If It Ain’t Repeated Addition, What Is It?

160 thoughts on “If It Ain’t Repeated Addition, What Is It?”

1. Great post. This is what is so wonderful about the blogosphere. Not only do I get to read great content but I get to read great reactions to that content. I think your post will achieve Devlin’s goals for his article much more easily than his actual article. Irony here is that there had to be the article so that you could complete the circle, and write your post that shows teachers how to incorporate in to their own psyche.

   As far as exponentiation. I suppose there is a picture with number of units in a dimension. Something like the multiplication diagram, but with more dimensions…. I am guessing at best.

   I think though that Devlins argument about “not repeated” may be even more salient with exponentiation after seeing students struggle with logarithms.

   Matt

   Reply

2. I agree with the idea of dimension. A line is x, a square is x^2, a cube is x^3 and so on. Just because we cannot visualize any higher dimensions doesn’t mean that they don’t exist.

   When presenting this to my class, I usually refer to the classic Simpsons episode when Homer drops into a 3-D world.

   I also encourage my students to imagine the “world” of kindergarden children. If you asked, the majority would assume that Natural or Whole numbers represented all the numbers in the world. Just because we can’t picture it, doesn’t mean it doesn’t exist!

   On another note, I still question the fallicy of “repeated” operations. What about the concept of “groups”. Four groups of three; one half group of three=quarters?? x groups of seven. Does that not work?

   Reply

3. I thought about dimensions, but that does not help my middle school students. With “repeated multiplication,” I can at least explain the exponent rules and make sense of negative exponents — but with dimensions, I can do neither.

   And what about fractional exponents? While my kids may have fun looking at fractals, I certainly cannot expect them to understand fractional dimensions!

   Reply

   1. How to write 0×0 in successive “addition” way in mathematics?

      Reply

   2. How to write 2×0 & 0×2 both in a successive addition way separately?

      Reply

      1. Well, two 0s would be 0+0, I suppose, but it’s hard to see how one might write zero 2s, or zero of any number.

         As soon as you move beyond the whole counting numbers (1, 2, 3,…), you get into trouble. The concept of “repeated addition” is definitely one of those “rules that expire” in math, even if it didn’t make the original list: https://www.scusd.edu/sites/main/files/file-attachments/13_rules_that_expire_0.pdf

         Reply

4. When I review exponentiation with my A-level groups (UK notation: 16/17 year olds), I build it up from repeated multiplication when looking at natural numbers as powers: a^2 is a times a, a^3 is a times a times a, etc.

   I then build everything else from there, using the key property:

   a^b . a^c = a^(b+c)

   Everything else flows from this property.
   We agree this forces a^0 to be 1.
   Then we see this means that a^(-n) must be 1 over a^n.
   So we now have exponentiation defined for all integers.

   Then we see that a^(1/2) must be a number whose square is a, i.e. ‘the’ square root of a, and similarly for a^(1/n). From this we can understand what a^(n/m) is.

   This is enough for the first year of A-level. The final question (which is fudged at A-level) would be to ask how to make sense of an irrational exponent. I talk about this by bounding it above and below by a rational number, and waffling about converging sequences. It also helps to introduce the graph of a^x, and talk about its desired properties (knowledge of differentiation is useful here).

   The key is that ‘exponentiation as repeated multiplication’ is there at the start, and is still there as a crutch for simple examples, but I try to get them to understand that it is much more general than that, and that in particular it has not been defined arbitrarily — we could not suddenly declare that a^(15/12) means something different without destroying all the key properties which we want from the exponent.

   I also try to build in a historical perspective — the exponential notation is only around 350 years old, even for integer powers, and it’s useful to see how some of the mathematicians of the 16th and 17th centuries struggled with finding a consistent way to represent something like a^15.

   I’m starting my own blog at the moment, and this sounds like an excellent seed for a blog post — thank you for the inspiration!

   Reply

5. This is much like what I do. The idea of repeated multiplication helps to explain/justify the basic rule, but from that point on, we work abstractly — working with the numbers and variables and exponent rules. Perhaps this is one of those places where learning to manipulate the symbols must come before understanding what they mean?

   I think that what I want is some way to tie exponents and logarithms together (my students always have trouble with logarithms) in a simple mental image. I just haven’t figured out what that would be.

   Reply

6. For me, exponents really emphasize the importance of definitions in math. When we first define a^n as repeated multiplication, there’s that little parenthetical requirement that students often ignore — namely, n must be a positive integer.

   Then we ask “What is a^0?” Students look back at the definition above, and try to fit this into that situation — “what is a times itself 0 times?” What they need to understand is that the initial definition says nothing about this — there’s no hint, there’s no tweak we can make, there’s nothing at all. So, the definition is lacking — it needs to be expanded beyond “repeated multiplication.”

   Then we do the same with negative exponents, fractional exponents and (less formally at this point) irrational exponents. All of this results in a sloppy patchwork of definitions — we’d like to find a simpler definition that covers all of these cases. Unfortunately, one can’t understand this definition really until integral calculus. Then we can tackle even irrational exponents.

   I don’t think there’s a way around starting with repeated multiplication, but I think it’s important to emphasize how that understanding of exponentiation falls short very quickly.

   To ramble on even more: This process reminds me of how science often works. We start simple (say, “The earth’s orbit is a circle.” ) We recognize insufficiencies in our understanding (“Mars is moving backwards.” ) We adjust our definitions to fit what we see / need (“Epicycles!” ) Eventually, the patchwork model we create is supplanted by a much simpler “truth” (“Ellipses!” ) I think this is a beautiful process that repeats itself over and over, and math often offers a way to follow this process from beginning to end, even if can take four or six years.

   Reply

   1. I know I’m really late to the party but…

      x^0 gives an opportunity to discuss the notion of Empty Product. 🙂

      The real collapse of the “repeated multiplication” explanation comes with non-integer powers.

      Reply

      1. I like the approach to exponents that James Tanton takes in this video: youtu.be/68I5vjZec2Y

         Reply

7. It looks like I got auto-emoticonned in the last post. Apologies.

   Reply

8. Todd, I added some spaces to your post to get rid of the smilies. Auto-emoticons can be very irritating; I wish I knew a way to turn them off.

   Reply

9. The original post has been edited to incorporate a comment from Keith Devlin.

   Reply

10. On how to represent multiplication:

    Euclid has a very explicit distinction between addition and multiplication.

    We represent numbers by lengths. You can add two numbers (lengths) together by creating a line whose total length is the length of the first line, plus the length of the second line.

    

    The result of multiplying two numbers a and b is the area of the rectangle with sides of length a and b.

    

    The nice thing about this representation is it makes the derivation of the formula a(b+c) = ab + ac trivial.

    

    The wrinkle, of course, is that it only works for positive numbers. We can then abstract out the key properties we want, and use this crutch/scaffold to work out what, for example, -1.5 times -3 *has* to be for our key properties to continue to hold.

    Reply

11. I have a blog article about Euclid’s geometric algebra in my queue — just have to finish the editing and paste in the graphics. Now, when I’m going to find time to wrap it up, I don’t know.

    Reply

12. I look forward to reading it when it appears! I didn’t look at Euclid at all until I finished university, and then only because I thought it was something that I *should* read.

    There are many other maths teachers, I imagine, who have never thought about geometry beyond the minimal amount of angle- and circle-theorem content in their curriculum… certainly in my country (the UK) ‘old-style’ geometric thinking is dead or at least very ill.

    Reply

13. Devlin unfortunately makes the mistake of thinking of multiplication as one “thing”. It’s true multiplication of any two real numbers cannot be simply reduced to repeated addition, however, the multiplication of any two integers *can* always be reduced (or thought of, or defined by) repeated addition. Even though we call them both “multiplication” technically they are different functions.

    In fact, we learn somewhere along the mathematical way that functions (like multiplication) are only properly defined by specifying their domain (among other things). Two functions that have different domains cannot be the *same* function. One function can be the extension or restriction of another, but they are not the same.

    This is the basis of the confusion. Multiplication of integers *is* repeated addition, in some form or other (Peano uses a recursive definition – recursive, repeated; I say to-mae-toe, you say to-mah-toe.) Multiplication of rationals is a different animal (related, but different.) Same for multiplication of reals, complex numbers, etc. All different functions even though they build on one another.

    Again, multiplication of rationals is technically a different function, in fact, an extension of multiplication on integers. Defining it requires that multiplication of integers has already been accomplished — and that, yes, means that repeated or recursive addition has already been put in the soup.

    The worst part of Devlin’s article was already alluded to in the original blog entry – he gives no coherent, compelling alternative – either definitional or pedagogical.

    Sometimes smart people are like that.

    Reply

14. I’d like to repeat a key point that I make: even Peano in his axiomatic defintion needs to define multiplication of whole numbers with a recursive (repeated) addition definition.

    That’s just the way it is and Devlin has not offered an alternative. Perhaps there is a way but he hasn’t shown any rigorous definition of multiplication that doesn’t at bottom crucially rely on the concept of repeated addition.

    The geometrical interpretations are nice but it doesn’t give you a way to rigorously define multiplication of integers. And it just a point of view anyways. One could always draw little boxes inside the rectangles and say: “See! Repeated addition of boxes!”

    Reply

15. And- let me be perefactly clear here, and say what the meaning of “is” is. When I say multiplication of integers *is* repeated addition, I mean they are one and the same function. The one you define in the ordinary way with repeated addition *is* the same function as the one everybody calls multiplication. Define it any other way and it still *is* repeated addition in that sense – it *is* the *same* function. Whereas, multilication of rationals is *not* the same function, by elementary function theory (i.e., they do not have the same domain – can’t be the same function.)

    Reply

16. “””The geometrical interpretations are nice but it doesn’t give you a way to rigorously define multiplication of integers.”””

    From the perspective of modern mathematics, where everything needs to be expressed in empty formalism to be rigorous, then you are perhaps correct, but it is certainly ahistorial to dismiss Euclidean geometry for lack of rigour.

    Reply

17. Well, I should have said it better, the geometrical interpertations are nice, and should be included in the discussion. Some aspects are clearer with the geometrical interpretations, especially perhaps the meaning of multiplication of real numbers.

    Students need to be given a symbolic definition of multiplication so they can calculate though.
    The geometric interpretation would seem to have practical limitations.

    Historically, I would have to guess multiplication for practical purposes such as commerce was not
    usually done geometrically.

    In the meantime it has come to my attention that some teachers have also been using Cartesian products (apparently called “ratio to one” ) rather than repeated addition . To illustrate 5×3 take a set with 5 elements, one with 3, form all possible pairs, and count how many can be formed. I guess that is clearly a way to define multiplication that does NOT rely on repeated addition, and it does precisely define the function (as opposed to saying – “just things you can do with numbers” !)

    Here’s a link to a study:

    http://eric.ed.gov/ERICWebPortal/custom/portlets/recordDetails/detailmini.jsp?_nfpb=true&_&ERICExtSearch_SearchValue_0=ED055773&ERICExtSearch_SearchType_0=no&accno=ED055773

    Reply

18. “””In the meantime it has come to my attention that some teachers have also been using Cartesian products (apparently called “ratio to one”) rather than repeated addition . “””

    Interesting, and links to a way of defining exponentiation in a way apart from ‘repeated multiplication’: the value of ‘a^b’ (with a and b natural numbers) is the number of maps from a set with ‘a’ elements to a set with ‘b’ elements. You can use this more generally to define 2^X, where X is any set, as the set of subsets of X. I’m not sure this, or the Cartesian product view of multiplication, is something I would use to introduce the topic in my teaching, though!

    I see that paper is from 1968, the hey-day of ‘New Math’… I sometimes wish that I had been teaching at that time, as the optimism exhibited in the teaching materials of the time is hard to find in modern textbooks.

    Reply

19. We use Cartesian products (although I didn’t know the name) as a counting principle to solve math contest problems — but only with students who already know multiplication. I don’t think I would want to use it as a definition of multiplication for my elementary students.

    Reply

20. “Two functions that have different domains cannot be the *same* function. One function can be the extension or restriction of another, but they are not the same.”

    It seems like this is a basic principle we want our students to understand, whether with multiplication or exponents or physics. We start with a simple definition, then we re-examine it and revise it as we learn more. So rather than just teaching the rules, we want to help the students see where these rules come from and why they sometimes change as we go along.

    Unfortunately, many of my students just want me to give them rules to follow. They “blank out” on the explanations — trying to follow all that is too much work. They don’t see that building a basic understanding of the principles behind the rules is easier in the long run than memorizing and retaining a list of steps to follow for every conceivable situation.

    That’s why I try to come up with simple images that capture the essence of the concept. If the students can retain the image, they have something on which to build future explanations.

    Reply

21. I agree, and I thought that the dissing of the concept of “extending previous understanding” was the most disturbing part of Devlin’s article. He chooses to characterize the teaching moment of shifting from multiplication of intergers to multiplication of rationals as some sort of sleazy sleight-of-hand rather than an illustration of a pattern that in fact occurs over and over again in the history of mathematics. Let me quote:

    ———————————–
    “And telling them that multiplication is repeated addition definitely requires undoing later.

    How much later? As soon as the child progresses from whole-number multiplication to multiplication by fractions (or arbitrary real numbers). At that point, you have to tell a different story.

    ‘Oh, so multiplication of fractions is a DIFFERENT kind of multiplication, is it?’ a bright kid will say, wondering how many more times you are going to switch the rules.”
    —————————————–

    Why not say to that bright student and the rest of the class:

    “Exactly. People started out multiplying whole numbers and figured out how to do that. When people needed to find a way to multiply fractional numbers they were very clever and found a NEW definition (that relies on and uses the old one), that works exactly so that when the fractions are reducible to whole numbers, you get the exact same results as the old way, but also works for fractions not so reducible. This is called ‘extending the function’ and it happens again and again in the history of mathematics…”

    That’s not sleazy negative admission – its a “teaching moment”!

    I’m not a world class mathematician, but I thought the exposition of Reimann’s work in the book “Prime Obsession” was glorious testimonial to the ability of Riemann’s mind to extend the work of Euler to complex numbers, and thus shed fabulous new light on the subject of distribution of primes. And its just another instance of the general paradigm of “function extension”. It’s an important concept. Teach it proudly!

    Reply

22. Here’s a question I thought might get some interesting responses: Suppose we go with the suggestion that multiplication should be taught as “scaling” as in the original article.

    OK – now, is the usual concept of scaling really powerful enough to explain what happens when you multiply two complex numbers?

    Remember that (the usual way) of interpretating complex multiplication is of multiplying the magnitudes, but also adding the angles of the two multiplicands (viewed as complex numbers in the plane with polar coordinates) .

    Does “scaling” as a concept capture this rotational aspect that only comes into play when we ascend to the domain of complex numbers?
    It doesn’t seem to for me, without doing semantic back-flips. I don’t know a way to view the rotation as scaling.

    The question is does this represent the same sort of “OK- new rules apply now!” when we go from reals to complex, even within Devlin’s suggestion of teaching multiplication as “scaling”. Or am I just missing something here?

    And if you do find a way to explain complex multiplication as “scaling” (I’d like to see it) – does it involve such a straightforward explanation that its clearly superior to the old way of teaching these matters?

    Reply

23. A good question! And one that ties in very well to the start of this discussion, because it indicates that rotation could be a useful analogy for exponentiation, with the angle representing the exponent.

    Reply

24. I thought about incorporating Devlin’s idea into my materials, and ran into a problem…

    http://homeschoolmath.blogspot.com/2008/07/isnt-multiplication-repeated-addition.html

    Reply

25. Another question:

    Quoting again:
    “Multiplication of natural numbers certainly gives the same result as repeated addition, but that does not make it the same …Telling students falsehoods …”

    I was always taught that if a function has the exact same values as another function for every element of their (identical) domains then it *is* the same function. In fact that was given as the very definition of function equality.

    Was I taught falsehoods? And if by some act of congress that’s NOT now the definition of what it means for two functions to be the same, please tell me, Prof. Devlin, what is *your* definition? What standard textbooks can I find *your* definition in?

    Reply

26. Here’s how I understand multiplication. I want to know how many pairs I can make.
    5 X 1
    I’d draw 5 horizontal lines and cross it with 1 vertical line and count how many intersections. I’d get 5 and that is the product.

    5 X 0
    I’d draw 5 horizontals and no verticals, note there are no intersections and get 0.

    1/2 X 2/3
    I’d divide a box in half and then thirds (so I now have sixths), draw a / on the 4 parts that are 2/3, a \ on the 3 boxes that are 1/2 of the whole and note than 2 out of 6 parts of the whole have intersecting lines. 2/6 is the product.

    Reply

27. To borrow from Winston Churchill’s comment on democracy, I wonder if repeated addition is the worst form of presenting multiplication, except for all the others.

    I ponder this in re-thinking middle school and Algebra 1 multiplication via scaling and so on. I miss the rectangles and arrays of blocks used to scaffold multiplication, and which then continue to serve in the distributive property. Kids have a way of resonating with tangibles. So I worry that I may be trading one aha! moment for another, or none. The new way, they discover “ooh, multiplication includes repeated addition.” The old way, they definitely intuited “I can extend integer multiplication to these other kinds of numbers.”

    I recall my crude gropings in meeting exponentiation involving non-integers, back when we scratched our calculations on birchbark. I supposed that guess-and-check could get a sufficiently useful approximation. A year later, I saw how exponentiation and trig could be calculated less haphazardly with series, and I even saw how some of these series related to the function definitions. That was a bit of an aha. In the intervening year my lack of deep understanding did not prevent me from learning useful exponent and trig properties. Today, expectations to learn (a^b)(a^c) = a^(b+c) and so on still precede expectations to appreciate McLauren series or other ways to define exponentiation.

    Reply

28. A more rigorous definition of multiplication is something close to what “Doctor Tom” wrote here (scroll down):

    http://mathforum.org/library/drmath/view/61066.html

    Reply

29. G Johnson:
    All kids love to play with blocks. That doesn’t mean they learn much math from them.

    http://www.sciencemag.org/cgi/content/summary/320/5875/454
    Also see

    This quote is sad but true:
    “Dr. Kaminski and her colleagues Vladimir M. Sloutsky and Andrew F. Heckler did something relatively rare in education research: they performed a randomized, controlled experiment.”

    Reply

30. Another rigorous definition (for whole numbers) can be given ala Giuseppe Peano (famous for giving rigorous axiomatic treatment to the foundations of math, including axioms for integers, as well as cool stuff like space-filling curves.)

    His definition is a recursive definition:

    [a] A x 0 = 0.
    [b] A x B’ = (A X B) + A

    Where B’ is “the successor to B” as defined in his axioms for integers. Note that this definition *uses* addition.

    I think at some point its important for students to learn that in math there is often a choice as to how to define certain functions or other mathematical objects.

    Its not the case that some are “true” and others “false” (as Devlin states) even when they give the same results.

    Reply

31. “G Johnson:
    All kids love to play with blocks. That doesn’t mean they learn much math from them.”

    http://www.sciencemag.org/cgi/content/summary/320/5875/454
    Also see”

    I’m guilty of also posting a link to a study (see above several posts) and I think they are fascinating. On the other hand I think one must pay very close attention to the age groups studied (what works best for 8 year olds and 12 years olds might be very different) and also have many similar studies repeated and tweaked to validate the findings and gain insight into which features of the study were truly seminal and which were incidental or even misleading.

    Reply

32. “All kids love to play with blocks…”

    There was an interesting discussion of that study here: Fractions are not about pizza. As to whether children learn math from blocks, that depends tremendously on the situation — whether we are playing or teaching, what topic we are discussing, how the blocks are used, what other connections are brought to bear on the concept, etc.

    What I want, as a teacher, is to find a few methods that work to communicate abstract mathematical ideas to my students, in a way that the kids will understand them well enough to be able to apply them in new situations. The children do not have to understand a concept perfectly at the level that a college math major would understand it, but they need the concept to stick in their heads well enough that they can use it to solve problems and can build other ideas on top of it.

    Reply

33. If we illustrate multiplication (for example 3 x 5) with an array showing dots arranged in a 3 by 5 array- drawn on a blackboard – well that’s already far more abstract than handing the students 15 buttons and having them arrange them ins a real physical arrangement.

    I think one problem in interpreting such studies is one may ingest the rule “abstract presentations work better” and go overboard trying to teach 4th graders Peano axioms and definitions!

    (Well, I don’t think anyone would actually do that – but I exaggerate to make the point.)

    Reply

34. “All kids love to play with blocks. That doesn’t mean they learn much math from them.”

    I quite agree. I have tried but found many manipulatives to be time wasted. Working with sketches of blocks is way more productive than actual blocks, though, as mentioned, age and other factors figure in.

    What about sequence of presentation? Do blocks, pizza, etc. best precede and stimulate discovery of general truths; or ought they follow and anchor previously-presented abstractions? Research I’ve read has mixed results with a whole lot of Hawthorne effect goin’ on.

    A practical hazard of emphasis on the abstract is mindless symbol manipulation. In that sense, problems involving rectangles or repeated groups could serve as a canonical check that the student has an adequately connected understanding.

    Reply

35. What we need are more randomized, controlled experiments published in real peer reviewed scientific journals and less reliance on hunches and personal experience.

    Reply

36. It all depends on what one’s definition of repeated is. If the factorial can be considered repeated multiplication then so is the exponent. By the same analogy, multiplication would be repeated addition.

    Free Help with Math

    Reply
37. Pingback: The Daily Planet » Carnival of Homeschooling #132: Let’s Go To The Ice Cream Parlor!

38. “What we need are more randomized, controlled experiments… and less reliance on hunches and personal experience.”

    That sounds modern and scientific, but I think it is realistically impossible. How in the world can a researcher separate all the factors — teacher skill & effort, student past history, various home/family emergencies that affect student performance (and which it is unrealistic to think will be equally balanced in all your groups), the Hawthorne Effect, and more. I don’t believe there is any such thing as a randomized, controlled experiment in education. It is too complicated of a system. A researcher who thinks he can even identify, let alone control, all the things affecting his experiment’s outcome is surely guilty of hubris.

    In the end, educational research is simply an anecdote, just like all the other “hunches and personal experience.” We believe it if it seems to make sense and ignore it if it doesn’t. (Consider the educational establishment’s wholesale dismissal of Direct Instruction, which has performed amazingly well in more than 30 years of research.) We take what sounds reasonable and try it in our teaching — but I at least will not radically change my teaching style merely because of an experiment, no matter how prestigious the journal in which it is published.

    Reply

39. Keith Devlin has posted a follow-up article:

    It’s Still Not Repeated Addition.

    Reply

40. “Keith Devlin has posted a follow-up article:
    It’s Still Not Repeated Addition.”

    Yeah – and he’s still WRONG.

    The problem is by Devlin’s view things like the Giuseppe Peano definition of multiplication “is just plain false” by his own words. Well, Peano was a respected mathematicican, even more so than Devlin.

    Another problem is Devlin’s suggestion about multiplication *really* being scaling doesn’t hold up when you go from reals to complex. So he’s still done in by his own argument.

    As far as his “system view” argument – which is new to his argument and not really presented in the original article, well, very nice, but it is just a view. It’s not a matter of “truth” and “falsity” (as much as he pretends it is). He can’t “prove” it “true” and other more historical views “false” that way Giuseppe Peano can prove various properties of multiplication of whole numbers once you accept his definition. If he wanted to promote a view, he should be direct and forthright about what he’s up to, and not try to use his authority to act as if this view were some kind of mathematical theorem.

    It’s all so much high-talking rhetoric to try to divert attention from his original outrageous contentions, such as saying that even though repeated-addition and multiplication give the exact same values for all whole numbers, they are NOT the same function (for whole numbers). This flies squarely in the face of the defnition of what it means for two functions to be the same. He can’t defend that, so he goes off into Hilbert Space.

    Reply

41. Devlin says in his new article
    “…What worried me … That it was okay to tell students something that is totally and utterly false…”

    This is exactly what is so wrong and offensive about Devlin’s last two articles. What does he mean by “false” here? Oh and not just false – “totally and utterly false”. What does he mean?

    Does he mean he can prove it wrong as a mathematical theorem? Does he mean it leads to inconsistencies? Does he mean he can show it wrong by calculation? By appeal to the Supreme Court? What then!

    (My best guess is that when Devlin says “utterly and totally false,” he means he doesn’t like the approach 😉 )

    But enough of that–putting aside his outrageous statements, the real gist is that he doesn’t like the development wherein one defines multiplication for whole numbers, then for integers (positive and negative), then for fractions by multiplying numerators and denominators, etc.

    OK – he doesn’t like it. He thinks it causes confusion later on. Does he *know* IT causes confusion? Well, he has personal experience, anecdotal, personal, experience.

    Statistical evidence? No. (Via personal communication he doesn’t.) Does his personal take on the matter factor in the confusion he may have engendered amongst his students with his own personal biases and animus surrounding the issue? No. (Obviously he confused a lot of people with his article, I suspect the same may happen with his students.)

    Is he wrong on whether teaching multiplication as repeated addition is a bad approach? (Which is a different question from whether it is utterly
    and totally false.)

    I don’t know. He may be right, he may be wrong. I’d like to see more evidence that there is a problem specifically regarding teaching multiplication as repeated addition in the first place (I’ll grant there are problems in teaching math, whether this is *specifically* a significant part of the larger problem — I’m not so sure.)

    One thing I do know — going around making outrageous statements about traditional teaching s being utterly and totally false doesn’t really help.

    Oh, and another thing, Kurt Godel basically showed that mathematical truth and axiomatic developments of theory were not one and the same. (And didn’t Euclid have something to say about axioms, etc?)

    Reply

42. “As far as his ‘system view’ argument – which is new to his argument and not really presented in the original article, well, very nice, but it is just a view.”

    I thought that view was strongly implied by the first article. At least, it came to my mind right away when I read Devlin’s statement, “Why not say that there are (at least) two basic things you can do to numbers: you can add them and you can multiply them.”

    I have no way of judging the mathematical merits of this argument, whether multiplication (of integers) is or is not repeated addition. I have mentioned before on this blog that I am not “good” at math. But clearly, something other than repeated addition is needed as we move even into middle school arithmetic, let alone whatever comes beyond that.

    And it does make sense to me that we should try as much as possible to teach with a long-range view. If we want our students to understand real numbers, at the least — and if there is a method for teaching multiplication which will extend to real numbers — then we should pay attention to it. I believe that thinking of multiplication as scaling (as “of” rather than “and, and, and” ) is that sort of method, transferring with ease to fractions, decimals, percents, and more.

    Reply

43. Denise says:
    “and if there is a method for teaching multiplication which will extend to real numbers — then we should pay attention to it”

    Well, yeah, I’m interested. But I just see a hunch so far, very unclear. Presumably its still a good idea to teach students, say, how to come up with the value of 12 x 13 without using calculator or looking it up in a table. Does your suggested drawing do the job? Does it do it better than showing a 12 x 13 grid? If I teach students to multiply fractions by using integer multiplication on the numerator and denominator to calculate the result fraction – am I just doing it wrong? (Because that implies that multiplication of fractions is “built up” from integer multiplication – something Devlin says is a no-no.) What’s the new way? Seriously – its just unclear.

    Mainly I’ve been reacting to the negative stance of Devlin’s two articles now. I think it’s damaging and irresponsible to say that the old way is “utterly and totally false”. One because its not, and two because I think such talk only confuses the issues more. I would be a very confused puppy if I were one of Devlin’s students and he said those things in class. I don’t think most mathematicians would even agree with him.

    Reply

44. I am not sure that my drawing does the job. That’s why I asked for more ideas!

    My experience has been that teaching multiplication as “of” is very helpful to my students. The drawing in the post above is linear, because I had the number line in mind. For many situations (such as fraction times fraction), an area model works better. But even there, I teach the multiplication as “a fraction of a fraction,” so it seems to me that the basic idea is still scaling.

    I would like to see this discussion move beyond negative reactions to how a person expresses himself. What I really want to know is, how can we best teach the math concepts — what methods work in communicating an idea from the teacher’s mind to the student’s, with a minimum of distortion?

    Reply

45. “I would like to see this discussion move beyond negative reactions to how a person expresses himself.”

    Well, Devlin’s argument itself is a strongly negative reaction to and condemnation of the way current teachers express themselves.

    So, I’m fully in agreement with you here. And I’d like to see more details on the positive part of his suggestion.

    Reply

46. I just read Devlin’s two articles rather quickly and have quickly scanned the blog here. Based on this quick look, I have some particular concerns.

    1. Devlin is ignoring the cognitive development of the students. Since elementary school students are largely “concrete operational”, we have to be very careful in how we teach arithmetic (and everything else). So, axiomatic approaches and other very abstract approaches are likely to fail the vast majority of elementary age students.

    2. The “multiplication is repeated addition” does work if we are only working over the nonnegative integers. Since this is the ring in which elementary age kids start their learning (again this is a very concrete setting), I am not offended by the idea that “multiplication is repeated addition.” [Recall that a “ring” is a set along with two operations and a collection of properties that are required for these operations.] Of course, this idea does not hold over other rings including the rationals, reals, or complex numbers. When students change from the ring (Z^+, +, *) to the field of rationals or the field of reals, there is a natural need to change the concept of the multiplication operation.

    3. In real analysis courses, the laws of exponentials are often proved by first starting with whole number exponents. Of course, this is the setting in which “exponentiation is repeated multiplication.” Then, work is done to expand the domain of exponents to the rationals, and finally limits must be used to prove that the laws of exponents hold for irrationals as well. This is what upper-division mathematics majors are learning. Again, I’m not so worried about the “exponentiation is repeated multiplication.”

    Finally, what I am worried about as a college mathematics professor? Where do I think these arithmetic and algebra deficiencies start?

    I think that overuse of the calculator is one of the great hindrances we are seeing. Students can compute nearly anything on those little machines, but they cannot explain it! Teachers in K-12 AND college professors should not accept this! The students must be able to compute on their own and WRITE out the computations carefully. My suggestion is to ban the calculator from most all of K-12 mathematics. Require computations by hand to develop number sense, skills with the order of operations, and skills with exponents. Require neatly written, mathematically correct statements to show what the students have done. (They should use “=” signs to create a string of equalities that hold true.) These experiences will make learning algebra much easier for the students.

    Don’t be fooled. I’m not “anti-calculator” or “anti-technology.” Indeed, I’ve always owned all of the top-of-the-line calculators and computer software for mathematics. But, I know from life as a faculty member and as someone who has developed computer software that (1) by hand computations and development come before implementation in the technology and (2) technology should only be used when it really helps students understand…and not just to please the administration. So, I do think calculators can be added for use later in science courses and even in mathematics courses. But, again, only when the calculator/computer is really helpful in the learning and does not stunt the student’s mathematical growth.

    Thanks for listening! I’ll be curious to hear your thoughts on this!

    Reply

47. My error — note that the nonnegative integers (denoted Z^nonneg) with addition and multiplication do NOT form a ring as I said in my previous post. Clearly, (Z^nonneg, +, *) does not contain additive inverses.

    So, elementary age children who are working in Z^nonneg are working in a set that is closed under both + and *. Moreover, these operations are associative and commutative in this set. Also, an additive identitiy and a multiplicative identity are contained in Z^nonneg. Finally, + and * satisfy the usual distributive properties. Thus, these children are working in a subset (but not subring) of the ring (Z, +, *).

    Sorry about the error!

    Reply

48. I think you are right that the problem is not so much in the very early years of learning multiplication. The crisis comes in late elementary and middle school, when students need to make the transition to rational and then to real numbers. At this point, I’m afraid, it is too easy for teachers to present multiplication as a set of arbitrary rules ( “multiply the numerators, and multiply the denominators” ) rather than as operations that make sense.

    It doesn’t help that many students only want to learn the rules, not to think about why they work. That “Just give me the facts, so I can get this over with!” attitude keeps them from building a foundation of number sense to support later work. This is the time that they need to be dropping their milk teeth and learning to chew real food.

    It also doesn’t help — and this is my understanding of Devlin’s argument — that many K-8 teachers are stuck with a milk teeth level of understanding as well. When we teachers think that multiplication is defined as repeated addition, without following that idea through and seeing where it falls short, then how can we help our students move beyond that?

    I agree with you, the prevalence of calculator use in elementary school hinders learning. Calculators should be banned in math classes at least until algebra, and I don’t believe they are needed even then. But kids feel grown up using a calculator, so I don’t mind letting them have a little fun after they have mastered arithmetic — especially in science classes, where the focus is on understanding the chemical reaction or projectile motion, not on the mechanics of number-crunching.

    Reply

49. The rule about multiplying numerators and denominators of course is not arbitrary and should’t be presented as such.

    It can be motivated many ways, including the “fraction of a fraction” approach.

    Reply

50. Denise,

    My previous post was largely to argue that Devlin was incorrect in saying that the techniques used by teachers were not acceptable in the mathematical community.

    You are right that Devlin is pushing for deeper understanding of mathematics by k-12 teachers. Educating mathematics teachers is a current “hot topic” and rightly so. They need strong backgrounds and good support. Moreover, we need to recruit teachers from the top of the class, provide salaries that compete with business, have good parental support, and restore their place in society to one of great respect. To help many of our cities recover from sad states of decline, boosting the educational system is the answer.

    In my own city, a strong school system would bring people back to the city/county and would attract great industry. We sit at the intersection of two interstates, are near a port, and are near a major city. There’s no reason we couldn’t be wildly growing and thriving…but we need a good school system to make that happen.

    Reply

51. Another math blogger argues with Devlin:
    Devlin On Multiplication (or What is the meaning of “is”?)

    Reply

    1. In case anyone happens to read that blog piece I wrote nearly 9 years ago, I quickly came to disagree with my own critique of Devlin’s arguments and have believed ever since that MIRA (“Multiplication IS Repeated Addition”) is a fallacy. Whether it “IS” any one single thing has been well-debunked here and elsewhere, but to teach children explicitly or implicitly that it’s ONLY repeated addition is to do them a serious disservice. Were I as thoughtful a child in the mid-to-late 1950s as my son was in the mid-to-late 1990s, I well might have asked, “Then why do we need multiplication? Let’s just do repeated addition and forget this “multiplication” nonsense. Life is tough enough already without cluttering up our lives with useless definitions, symbols, and procedures.”

       That’s a somewhat tongue-in-cheek pseudo-question, but there is likely at least one reason for making multiplication a distinct operation from addition, rather than “just doing the same thing as before, more times.” I don’t know that some of the people who so fiercely disagree with Devlin are fanatical believers in and/or purveyors of MIRA in its purest and most inflexible incarnation, but they surely do seem outraged by what he wrote in ’08 and has periodically revisited since. I do wonder what fuels their spleen exactly.

       Reply

       1. Well, some of us (human beings in general) just enjoy arguing. 🙂
          For me, the MIRA slogan provided a mental hook that I could hang simple arithmetic concepts on. It worked well, to a point. And so I passed it on to my kids, not really realizing its limitations.

          Then Devlin’s article forced me to consider the topic more deeply. And the longer I looked, the more problems I saw with MIRA. The worst fault being that the slogan glosses over important ideas like rate and proportional reasoning. Thus it doesn’t provide the understanding students need when faced with an unfamiliar math situation.

          Reply

52. So, we start kindergarten by talking about an infinite set of ordered things, each with a successor?

    And that there are two operations we perform, pairwise…

    The Devlin piece was non-serious.

    Jonathan

    Reply

53. That was too brief. Repeated addition is multiplication, and that’s where we start…

    We refine, we extend, we don’t need to correct.

    Same thing happens with exponentiation (except teachers hand wave over x^1, which we really, really should not do)

    Jonathan

    Reply

54. Come on, guys! Mocking Devlin by talking about teaching kindergarten arithmetic as “an infinite set of ordered things, each with a successor” is being non-serious.

    Multiplication is equivalent to repeated addition only in the natural numbers. With a bit of fudging about what a negative sign means (how can we add something a negative number of times?), we can extend it to the integers, but that level of understanding will not even get our students through 4th grade. Yet we teachers repeat it like a mantra, over and over again, until we think it is a universal definition.

    That attitude might be defensible if there were no simpler way to teach multiplication to young children. But there is a simpler method: multiplication means “of.” And that little word has enough “refining” and “extension” built in to cover operations with the rationals and even the real numbers.

    Miquon Math teaches multiplication by fractions in the first semester of first grade using this method. Children can understand it. It’s easy. Why do you argue so strongly in favor of a less-general alternative?

    Reply

55. I don’t think there is a big gulf between repeated addition and the word “of”. “Copies of” can be used to explain 3×5 as 3 copies of (units of) 5 = 15 total.

    You can use it for fractions too – 3 1/2 x 5 is the same as 3 and a half copies of (units of) 5.

    Once one has accepted Devlin’s unsubstantiated premise that teaching repeated addition causes some crisis later on – which I am dubious of – then one may start fretting about all these things that work just fine.

    Use the word “of” , use “copies of” , use repeated addition, use grids of dots, or use even cartesian cross products pairings – they all work in some situations and need to be extended or redefined in others. Even Devlin’s “scaling” concept falls short with complex numers. The student who begins to see that they are all different perspectives on an underlying truth is learning to see math as it truly is. And here is another really deep truth – no perspective is the whole truth.

    I don’t have the Miquon Math materials but by their advertising description they are in favor of the multiple perspectives approach.

    Devlin on the other hand thinks that he can say which perspectives are right and which are wrong.

    Reply

56. Denise,

    I intended my second post to supersede the first, which was inappropriately flip.

    But let me be clear: Devlin’s column was non-serious. Look at this:

    Why not say that there are (at least) two basic things you can do to numbers: you can add them and you can multiply them. … Adding and multiplying are just things you do to numbers – they come with the package. We include them because there are lots of useful things we can do when we can add and multiply numbers. ….

    He’s just wrong. This is neat stuff to share with people who already know math, but it would lead to real problems if teachers needed to use it to inform their instruction.

    Little kids live in the real world and, mathematically, in the natural numbers. We can carefully abstract (natural) numbers and then addition, and then multiplication from the world. Repeated addition does the trick, and does it well. We should be careful to avoid saying that multiplication is identical to repeated addition, but that should not scare us away from saying that repeated addition is multiplication (or is equivalent to, if we are not concerned with sounding pedantic).

    Now, if you are concerned with your middle school kids, you have a chance to refine, make more precise, extend… But I don’t think that’s where Devlin’s article was targeted. (Actually, I don’t think it was aimed at teachers at all. I think he wanted to get a rise out of mathematicians and math-able laymen).

    Finally, the “of” trope can be a useful tool, it can help. But as it fails in many other languages, it really can’t be more than a neat trick in English. Mathematics is universal, “of” is not.

    Jonathan

    Reply

57. I think Devlin was serious – and seriously wrong.
    Sometimes people – even very smart people – harbor these little bugs — an “animus” (plural animi?) — that make them irrational when their little bug acts up. I think that’s what’s going on.

    And riffing off the previous post, imagine a student taking a test: please define multiplication — answer: just something you can do with numbers; define exponentiation — answer: just something you can do with numbers; define integration — just something you do on functions… and so on.

    By the way – how *do* we teach integration then? I always thought of it as a kind of fancy addition … (and yes there are more abstract definitions… )

    Reply

58. Back before Euclid, mathematics was empherical, which means table driven. The priests had the tables, so you had to go to a priest to get the answer to things like muliplication problems.

    We learned our multiplication tables. Sure, it was easier to add stuff up over and over again, but we learned the tables, and the tricks. At some point the tables became implicit, and we never had to think about them or adding stuff up.

    I’ve never gotten to the point where I instantly know what 23 squared happens to be.

    I do remember stopping at a convenance store late at night where a guy was learning the GED version of percents. They have to remember three different equations and the situations leading to the use of one or the other. Algebra makes the cognative load so much lower. I can construct the formulas quick enough, but they are not implicit for me. They might actually become implicit to him.

    Likewise integration of trig functions. Just memorize the stuff. I didn’t and it has taken me forever to do what is now, post memorization, easy enough.

    At some point understanding the system at one level gets in the way of understanding it at another. It works both ways known to the yet to be known, and known to the forgotten–learning, or teaching.

    Reply

59. Jonathan,

    English may have an advantage, in that we have a simple, two-letter preposition to represent the idea, but every language must have some way to talk about measurement of a continuous quantity by a scale unit:

    AxB = “A units of size B.”

    Joe,

    Allow me to present my understanding of good pedagogy:

    One clear definition
    + Multiple representations or applications
    = Understanding

    It seems to me that you are saying the multiple representations alone are enough, but I think that will leave the students (except for a few who can abstract their own definition) wallowing in confusion. The teacher needs to have in mind and to present a single, clear definition which will stick in the student’s mind — and then all those multiple representations and applications need to be grounded back to the definition.

    Part of the teacher’s job is to find the strongest, clearest definition possible. For years, elementary and middle school teachers have used “multiplication is repeated addition” not simply as one representation among many, but as the foundational definition of multiplication for their students. I am arguing that it does not work well in that role.

    I am not concerned at this point about teaching complex numbers. I just want to teach my kids to handle the real number system with confidence and think their way through problems within that system. I’d even be satisfied to bring them to true competence with the rationals. Let tomorrow worry about complex numbers.

    Reply

60. The discussion continues to spread. Text Savvy weighs in with:

    Devlin’s Right Angle, Part I

    Devlin’s Right Angle, Part II

    Reply

61. Denise,

    in some declined languages grammatical case plays the role of “of.” In Russian, the case will depend on the number, with different choices for 1, 2 – 4, and 5 and above.

    In Turkish, I think the closest you will find to “of” is a nonce word, “tani” which means something like “pieces” or “occurrences” and probably falls closer to “times” than “of.”

    Let others chime in, correct me if need be, but I would be surprised if this model holds for more than a few related languages.

    Jonathan

    Reply

62. Denise,

    I could respond at length – I don’t think I really disagree with you in principle, (although I do disgree with Devlin in principle on matters of truth and falsity,) and I think clear definitions are essential at some point (but not very early on.)

    But let’s cut to the chase – what is your one clear definition of multiplication that works for reals (or even just rationals) that you can present to a 8 year old as their essential introduction to multiplication?

    I’m not trying to put you on the spot – but the stuff that has been said about scaling and “of” doesn’t quite fulfill my expectations for a definition. So I’d really like to see a more definitive presentation of this crucial point. If you want your diagram to be part of the definition I’m fine with that. It kind of presupposes that the child already can conceive of a number as a length (or an area) and I’m OK with that too – though that implies that these related concepts are taught in some sequence that makes sense (as always).

    Given that definition, we can perhaps all explore whether we think it will really hold up in the real world of teaching *all* children (not just above-average children).

    I mean, part of the uproar (only part) is caused by Devlin’s lack of a truly clear, compelling, and decently worked out alternative, that seems like it will fly in the classroom.

    ——–

    On Text Savvy’s article (Devlin’s Right Angle) – I have to point out that the claims of the opposing side have be distorted. Quoting Text Savvy he says “all multiplication IS repeated addition” – Nobody is saying that! What I am saying is that for whole number (or for integers), yeah, you can define it that way and it works fine. You could also define it other ways and it can work out fine. Argue with Giuseppe Peano if you think it doesn’t work. When it comes to rationals, yes, you need a new definition — but that’s a valuable lesson in itself about how mathematics works — not an ugly about-face and defeat.

    Reply

63. By the way, my pointing out that Devlin’s fuzzy suggestion for how to teach “the truth” fails for complex numbers is to point out a matter of principle. In this matter I’m concerned with how Devlin is using (or abusing) language, his authority as a mathematician and public figure, not with what “works best” for elementary or middle school students.

    He is abusing language when he talks about the “truth” and “falsity” of various approaches, and then goes on to suggest his way is “true” and the way he doesn’t like “false” – even though his way “fails” in the exact same way (albeit at a later point in time). It’s hard to fathom whether he is really just that confused or just that arrogant.

    That abuse of language and authority is both damaging and confusing. And I suspect his students may be very confused, not just because of their prior education, but also by what they may hear from Devlin on these sorts of meta-mathematical issues.

    Reply

64. Full disclosure –

    I learned multiplcation (for whole numbers) at age 5. My dad drew dots in an array to explain. Saw it immediately. No problems then or later on when approaching fractions.

    Anybody else remember exactly when they were introduced to multiplication?

    Reply

    1. Are “dots in an array” merely repeated addition? Is “area” repeated addition? Is matrix multiplication repeated addition of matrices? I could go on, but I knew long before July 2008 that arguing with Joe N. is a fool’s errand. Still, it moves.

       Reply

65. My definition: To me, the number line seems the best representation of the real numbers, so my definitions of the arithmetic operations are based on the number line. I described my definition of multiplication as scaling in the last section of the article above, “Edit: A comment from Devlin.”

    I do not teach that definition in that way to early elementary students, because they are not yet used to the number line. But it is always in the back of my mind, and I tie each multiplication calculation into it. For example:
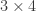    = “3 of the 4s.”
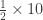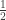    = “ of 10.”

    In middle elementary, bar diagrams like those shone above represent a “thickened” chunk of the number line. I have talked about how I use those in several past articles.

    Gosh, I must be old. I have trouble remembering last year, let alone when I was five!

    Reply

66. I think I teach it pretty much same as you (although I *still* like dots in a grid) . We may have differing interpretations of exactly what Devlin is proposing – which is why I continue to disagree with him!

    In my view, saying “3 of the 4s” or
    3 copies of (groups of) 4 – or
    3 sets of 4 each, etc.

    — all retain a strong flavor of repeated addition.
    After all, one must count or “add up” all the resulting copies.

    On my memory – thanks to this discussion that memory came back to me and i appreciate that!
    It was at the kitchen table – clear as a bell now.

    He also showed me (in the very first lesson) how you could group those dots either vertically or horizontally, and thus it was also an introduction to adopting differing perspectives.

    The reason my dad showed me these things was because my older brothers were already into multiplication and I was envious.

    Reply

67. And I think, but could not swear, that I used arrays of dots.

    I also think I had guided play with square blocks (encouraging an area model of multiplication).

    I do recall doing long multiplication in third grade, procedurally, so the concept was already there. In fourth we had flash cards (had to make them ourselves) and we had to know all the one-digit facts. (I still paused for 6×7, 6×8, 6×9, 7×8, 7×9 and 8×9, although I knew commutativity without thinking, so just 6 facts). I do recall recovering a missing fact like this:

    7×6, hm, 6×7, hm, 5×7 is 35 and one more 7 makes 42

    Makes me think I was taught repeated addition at some point.

    In second grade there was an awful lot of distribution and rewriting numbers in expanded notation. There was a lot of number line stuff. And I think, strangely enough, there were negative numbers. Not that any of this was taught to us. Open classroom. Me and Martin used to go to the math corner and work independently (lesson on a 4×6 card, maybe it was bigger, with some questions at the bottom. Get them right – check the back of the card – and take the next card. I think we got chased away for spending too much time there. And I think we worked through 3 years of highly New Math flavored cards in one year.)

    And I guess, in the end, I was exposed to lots of presentations of lots of kinds of math, multiplication included. I love those arrays. Seven rows of 6 dots each, 7×6 is 6+6+6+6+6+6+6…

    I’d hang my hat on some combination like that.

    Jonathan

    Reply

68. “7×6, hm, 6×7, hm, 5×7 is 35 and one more 7 makes 42”

    Beautiful!

    I show my (curious, more advanced) kids how to use this kind of mental “distributivity” to multiply any two digit numbers in their heads.

    What was once common is now a parlor trick.

    Being successful though sort-of assumes they have memorized 1 digit multiplication though (to help relieve the burden of carrying too many partial results in memory.)

    If you can keep a bunch of partials results clear and separate in your mind, you can advance to 3-digit in-the-head.

    Reply

69. I found that using multiple models (bad pun, I know) to define multiplication is the most empowering for kids. Repeated addition becomes one model out of many, including splitting, “fractals”, symmetry, area, or particular applied models such as time and money. My company made a poster summarizing twelve most popular models, which you can find here:
    http://www.amazon.com/exec/obidos/ISBN=0977693910/naturalmathA/

    However, I realized that the task of coming up with multiplication models, or trying to answer, for yourself, the definition question “What IS multiplication?!!” is too much fun to provide any ready answers. So, we made a piece of software where users can collect multiplication models online – a kind of a community art project helping to define multiplication. It’s now in closed beta, but it looks like we will be opening it to the public pretty soon.

    I am yet to find a good definition of multiplication. The formal definition is unteachable and the textbook definitions are wrong. A big fat collection of handmade models is the best I have by the way of definitions, so far. Which redefines the notion of “definition” in a sense that is too social for some people’s tastes, but well.

    Reply

70. I would like to add that MariaD is one of the authors of my favorite online multiplication tutorial. I like it because it captures exactly the playing-with-concepts attitude I try to teach my students.

    In fact, the tutorial is very like what I wrote years ago on a homeschool forum. I’ve been meaning to rewrite that post one of these days. Perhaps this discussion will spur me to pull it off the back burner. Although I don’t know whether I should bother, when I can continue sending my friends over to the NaturalMath site.

    Reply

71. I have my old math books (from Finland) right here, so I checked them. It was interesting!

    Multiplication concept was introduced in the fall term of 2nd grade.

    The first page in that chapter asks the student to WRITE the word “koti” two times, the word “koulu” three times, etc.

    The next page asks the student to DRAW
    2 times a set of three elements
    3 times a set of five elements
    etc.

    The next page has pictures of dots inside ovals, or sets with the same number of elements and student is supposed to fill in the numbers on the empty lines; under each picture is ___ times ___

    Next page defines multiplication. It says 2 . 5 means “2 times a set of 5 elements”.
    The student is to draw sets with elements to match multiplications such as 3.5 or 3.2 or 1.6

    On the next page is more practice in writing a multiplication from a picture of dots inside ovals, such as 4 . 2 (but no total)

    Then one page with money pictures, to write for ex. 4 . 5p or 7 . 10 mk (but no total)

    Next page, it shows the equal sign the first time (with multiplication). It talks about finding “how many together”. Student either writes multiplication equation from the dots in groups pictures, or vice versa, draws groups to match 3 . 4 = ___.

    THEN on the next page the students write BOTH multiplication and addition equations from the given dot pictures. That is practiced for many pages then.

    Some later, a rabbit jumps repeated jumps of three on a number line and there’s some practice on the table of 3. Then similarly for table of 2 and table of 4 (shows the rabbit jumps)
    And the chapter ends.

    All in all the definition was as “so many groups of so many elements”, and it was connected with addition only after 8 pages of work.

    It was clearly not defined as repeated addition. It was not tied in with very many models, either. Only the dots/ovals and number line jumps at this point.

    In the spring term of 2nd grade and then in third, the exposition was quite similar but of course went on to the times tables practice and the “long multiplication”. It even listed as a goal that the student knows the “connection” between addition and multiplication and can use that to find products.

    I don’t know what the teacher’s edition might have instructed on the matter.

    Reply

72. “It was clearly not defined as repeated addition. ”

    See – I don’t interpret it that way. If you draw these sets and groups of (dots, coins, what-have-you) you still have to add them up.

    Personally I think the material described sound fine – I just wonder (and I’m truly in the dark) as to whether such approaches would meet Devlin’s approval. Such approaches have been used for years, decades, maybe centuries.

    Is Devlin really only concerned with an approach that says “muliplication is repeated addition– PERIOD.” and no further discussion/illustration? I don’t think so.
    Otherwise it would be a pretty meager point he was trying to make, because almost all materials I’m familiar with take the “multiple models” approach.

    I think he’s objecting to any approach that introduces multiplication as an discrete operation on discrete elements — which then at least implicitly if not explicitly involves summing up the elements — and therefore all these approaches (grids, sets of multiple elemnets etc.) fail the “Devlin Test“.

    Reply

73. Looking at the Natural Math models for multiplication – I wonder which ones Devlin would approve of. Clearly repeated addition is out – which ones are in?

    Reply

74. One thing I must thank Keith Devlin is he included the link to this wonderful blog. Unfortunately, I come to this discussion a bit late, so I only glanced at all of the comments so far, and I probably haven’t digested all the details.

    I actually agree with the essence of Devlin’s column, but my reasoning might be slightly different. But, before I get into that point, I just wanted to briefly talk about my “philosophy” about elementary mathematics teaching and learning.

    To me, most, if not all, of elementary school mathematics teaching/learning involves abstracting mathematical ideas from concrete activities/phenomena. So, starting with concrete situations is essential for students’ learning. Therefore, teaching of multiplication, as it is typically done, probably should start with equal group situations such as 4 baskets of 8 apples in each. Multiplication is an operation that represent this situation in the statement, 4 x 8 = 32.

    Some might say, “see multiplication IS repeated addition,” but I would say “repeated addition” is A way to find the product, but not the essence of multiplication. To me, understanding multiplication, or thinking multiplicatively, means you can look at 8 as 8 “apples per basket,” not “8 apples in this basket, 8 apples in this basket, 8 apples in this basket, and 8 apples in this basket.”

    Going from “8 apples” to “8 apples per basket” is a huge cognitive step, and I’m not sure how many of 8/9 year olds who encounter multiplication for the first time make that jump at the time they are introduced to this idea. But, saying “multiplication is/as repeated addition” does not encourage students to move to that perspective.

    I think that’s what the textbooks from Finland (?) Maria was emphasizing, I believe. Japanese textbooks approach multiplication in a very similar manner, too.

    JN earlier stated that 2 functions with different domains can’t be the same, and I think that says clearly that multiplication and addition are two distinct functions, even with whole numbers. One of the important ideas about addition students should understand is that you can only add two numbers that are referring to the same unit (apples and apples). That’s the reason when we can simply add ones and tens to add two 2-digit numbers. However, multiplication does not have such restriction. In fact, when you multiply 4 and 8, you are multiplying “baskets” with “apples per basket.”

    Finally, Japanese textbook use an interesting diagram called double-number line (or proportional number line) to represent multiplicative situation. There was an article in May 08 issue of Teaching Children Mathematics by Beckman and Fuson that mentions briefly about such a model with respect to multiplication and division of fractions.

    Thanks again for a very stimulating discussion.

    Reply

75. Hi, Tad, and welcome to the discussion! I’ve been following it all along, and I know I haven’t digested all the details.

    No one else (as far as I can remember) has mentioned looking at the units on each number — and you are right, they’re not the same, nor do they match the units of the product. The concept of a “this per that” unit (such as “apples/basket” or “grams/cubic centimeter” ) is very important for students to understand.

    Reply

76. I have described the example of 1/2 X 2/3=2/6. I have “Elementary Mathematics: Its Structure and Concepts” by Margaret Willerding and she gives a visual demonstration of this as well as the more complicated 3/2 X 5/3.

    This may also be helpful:
    http://thinkmath.edc.org/index.php/Multiplication

    Reply

77. The above comment by ari-free was actually posted on 7/9, but Akismet mistook it for spam. I just discovered it and performed a rescue, changing the date and time so everyone will have a chance to read it.

    Reply

78. The link ari-free gave us is interesting in that they, too, say multiplication is not repeated addition. They are basically using the Cartesian Product approach to multiplication.

    Although we do see some combination problems in the 2nd and 3rd grade textbooks in their multiplication unit, I tend to think it’s better to start with equal groups. It’s much easier to conceive combination situations as equal groups than vice-versa. Moreover, I’m not sure how they plan on extending the meaning to fractions/decimals/negative numbers. IMHO, the major weakness of the Cartesian Product as the starting point is that it restricts the factors to be whole numbers. Maybe I am missing something.

    Reply

79. So what is multiplication, then, if it is not repeated addition? Dr. Devlin never really says. He instead asserts that addition and multiplication are two distinct operations that can be performed on numbers and mentions that children should get to discover or else be told that multiplication “gives you a super quick way to calculate a repeated addition sum.”

    Actually, we are first given the parable of the bicycle and the car, in which we are informed that these two distinct modes of transportation can both be used to get Dr. Devlin to work in about the same amount of time, and this should make it clear that times is not the same as repeated plus. What a terrible analogy! What he should have said is that riding his bike for one block, five times in a row is not the same as riding his bike five blocks, even though they have exactly the same outcome.

    Did I just miss something? Are we truly having a semantics argument over the meaning of the word “is”? So let me get this straight: Multiplication acts in every meaningful way like repeated addition, can be calculated in that way, but should never be thought of as repeated addition. Why is the phrase “fatuous pedant” suddenly stuck in my mind?

    Here’s where I’ve seen this pattern before. When I was very young, I learned that the Earth was a ball, and it went around the sun in a circle. Later in my wide-eyed youth, some mind that was clearly greater than my own (I think it was my older brother) established his intellectual superiority by informing me that the Earth was not, in fact, a sphere because the equatorial diameter exceeded the polar and one hemisphere bulged more that the other, and that the Earth’s path around the sun was elliptical. Can you imagine my embarrassment at my naivety at that moment? Here I was learning that the Earth was shaped more like a pear than a ball and our path around the sun was squashed like and egg. Only much later did I learn that the Earth is more spherical than a billiard ball, and the eccentricity of the Earth’s orbital ellipse is so close to zero that it is more perfect than any circle any of us has ever seen drawn or inscribed in any book or on any surface in our entire lives.

    The simple truth is that the Earth is a sphere and its orbit is a circle. Any quibbling on these points can be offered later for individuals who are majoring in astrophysics once their understanding of conic and hyperconic sections and astronomical distances has advanced to allow them to have some concept of the scale of these absurdly-minuscule departures from idealism.

    Multiplication is repeated addition. Save the righteous academic quibbling for serious peer-reviewed treatises. Young students don’t care at all for the majesty and awe of mathematical theory; when you introduce multiplication to them, they want to know what it’s good for and how to picture it. Addition was easy to picture; it’s only logical to use addition as a stepping stone for multiplication. No harm is done in this. As Dr. Devlin conceded, the two behave identically. Even when we dare to stray outside the naturals, three times pi is precisely the same as pi plus pi plus pi, and five-and-a-half times one-half is really five-halves plus half-of-a-half. The rules don’t change later; the association continues to work just fine. The word “is” saves paper over “behaves precisely the same in absolutely every imaginable context as.”

    When I was first learning multiplication, aside from being annoyed that I had to do it at all, I was happy to be informed that there was a short-cut to the repeated-addition problem. This idea didn’t stunt me when I was learning geometry or trigonometry or calculus or differential equations or linear algebra or set theory or quantum mechanics. In fact, I employed the “repeated addition” identity successfully and usefully in every one of those subjects.

    Teachers, please don’t take Dr. Devlin’s advice. We have far greater problems with education than K-through-12 teachers not falling in line with overly-pedantic mathematical dogma.

    Reply

80. Denise,

    The RationalMathEd post that you link to above has left me a little disgruntled, as he has said just about everything I was trying to put into words in a post I was writing, in a much more eloquent way than I can manage!

    We have descended a little into the realms of ‘what the meaning of ‘is’ is’ here, but I think (agreeing with the RationalMathEd writer) that Devlin misses the importance and power of metaphor. When we say that ‘multiplication is repeated addition’, we mean that we are using repeated addition as a grounding metaphor for a new concept, which we can than extend. Learning multiplication, just like learning anything else in mathematics, is a process of using grounding and linking metaphors as a bridge from material we are comfortable with into unknown or unfamiliar realms.

    So, multiplication *is* repeated addition.
    Multiplication *is* scaling.
    Multiplication *is* finding area.
    Multiplication *is* the cartesian product.

    All of these metaphors allow learners to access multiplication. They are not just scaffolds to be thrown away once the concept is ‘properly understood’, but connections which need to be integrated into a pupil’s more complete understanding of multiplication.

    Reply

81. I don’t think no one is arguing against the use of a metaphor. I have already stated that I agree with Devlin that saying “multiplication is repeated addition” isn’t good – though my rationale may be different.

    However, ultimately, I have no control over what actually happens in classrooms, and many teachers will keep saying “multiplication is repeated addition.” I just hope that they actually articulate and elaborate on why “repeated addition” is an appropriate metaphor. It is NOT because it gives the same answer, but it is because we have multiple of equal addends, i.e., we have equal groups. A sad reality of today’s classrooms is that too many students (and teachers) are focusing on the answers. Thus, I’m afraid too many students will simply focus on how to get the answers to multiplication instead of what multiplication is about.

    Reply

82. Jon, good post, agree with your sentiments, but I’d cede even less ground. And I don’t quite understand your use of the word metaphor in this context.

    To me multiplication (for whole numbers or integers) *is* the same function as the one you can define appropriately with repeated addition (as well as other ways) because that’s exactly what it means (that’s the standard definition) for two functions to be the same. **

    I put that to Devlin directly and he flat out denied it. He said yes the values are the same but the functions are not the same. Just totally at odds with very standard mathematical definitions (such as functions, equality of functions, etc.)

    He speaking as some kind of mystical oracle or guru — and we are supposed to divine the meaning through long contemplation, but his deep truth he is in touch with is not accessible to our ordinary rational minds.

    Thus I see all kinds of posts trying to divine the meaning – as people saying for instance that (maybe) Cartesian products or saying “5 groups of 4 apples” may be OK by Devlin.

    I don’t know about all that – I think all those approaches are fine – but only the mystical mind of Devlin ultimately can tell you what *is* and what *isn’t*.

    ————-

    **
    (I’m not saying that’s necessarily the *best* way to introduce it to kids – arrays of dots worked fine for me – but I had to add them up to get the right answer.)

    Reply

83. Great post David – but the punch line is good enough to repeat:

    “Teachers, please don’t take Dr. Devlin’s advice. We have far greater problems with education than K-through-12 teachers not falling in line with overly-pedantic mathematical dogma.”

    If it ain’t broke don’t fix it!

    Devlin thinks teaching of multiplication is broke, but I’m skeptical.

    What are better statements about what is really going on in elementary math education that produces the kind of galzed-over, clueless, shut-down, blank expression students that arrive in middle school?

    Reply

84. Joe,

    I am not a professional mathematician – I am a math educator whose primary interest is elementary/middle school mathematics education. Moreover, as I have posted earlier, I actually agree with Devlin. From a very pure mathematical perpsective, I don’t see how you can say addition and multiplication are the same function. I mean functions f and g are the same if f(x,y)=g(x,y) for all (x,y), correct? , so how can addition and multiplication, which are both binary operations, can be the same function?

    But, from a much more practical perspective, I also think saying “multiplication is repeated addition” isn’t helpful. Clearly, a major motivation for multiplication operation is – 4 baskets of 8 apples give us 32 apples altogether. However, the essence of multiplication we want children to understand is the “equal groups” and looking at 8 as 8 “in each basket” or 8 “apples per basket.” Afterall, even if we have 4 baskets, if 2 contained 8 apples, 1 with 7 and 1 with 9 apples, we still have 32 apples altogether yet we don’t have a multiplicative situation.

    Too often, you see those middle school students with “galzed-over, clueless, shut-down, blank expression” is because they focus solely on getting the anaswers. To them, multiplication is nothing more than computation that demands an answer, and repeated addition is good enough, don’t bother why. As a result, they do not develop the ability to think multiplicatively, which is the major focus in any middle school mathematics curriculum.

    I tend to think mathematics education in the US needs a lot of work – at all levels, just as much at HS and college levels. Teaching of multiplication isn’t an exception.

    Reply

85. Hmm.. Sorry about another post, but I tried to enter “less than” and “greater than” symbols in between 3×4 and 3+4, but it didn’t show up. I hope it is obvious that I meant 3×4 isn’t equal to 3+4.

    Reply

86. Fixed it for you, Tad.

    Reply

87. Joe,

    And I don’t quite understand your use of the word metaphor in this context.

    I am in the middle of reading Lakoff’s ‘Where Mathematics Comes From’, which uses ‘metaphor’ at least twice on every page, so it must have bled through into my writing :). Lakoff uses ‘metaphor’ to mean any relevant connection the brain makes between mathematical schemas, or between the real world and the mathematics under investigation.
    In this context, it would mean that ‘repeated addition’ is a possible way to start thinking about multiplication.

    To be charitable about Devlin’s article (particularly the second one), I think he is trying to argue that we shouldn’t teach anything to students which contradicts ‘the way things really are’, by which he means the axiomatic presentation of fields, integral domains, and so on. To me that demonstrates a limited world view, and an overly simplistic model of mathematical progress and development.

    Reply

88. Tad syas:

    “Joe…I don’t see how you can say addition and multiplication are the same function.”

    I’m not saying that at all. I’m saying you can have a definition of multiplication (for whole numbers or integers) that uses addition.

    You can refer to a previous most of mine that gives the Peano recursive definition of multiplication that uses addition. You can do it more informally by saying that MxN (M,N integers) denotes a function whose definition is given as MxN = M+…+M (N times). That’s all anybody means when they say that.

    Then, the function so defined and the multiplication function have the same values for every element of their given domains (which is technically pairs of whole numbers or pairs of integers). Devlin admits that, but says they are still different functions.

    He won’t give *his* definition of function equality, well, because I suspect he doesn’t have a *mathematical* definition in mind.

    Use the Peano definition if you like something
    more rigorous- exact same point.

    Reply

89. Tad, you seem to be among the group that thinks
    that something like “4 baskets of 8 apples” is a formulation that passes the Devlin Test.

    (Forgive me if I’m wrong here.)

    As I’ve said repeatedly – I’m fine with the approach.

    However, Devlin’s articles, as a confused and confusing as they are, do at least hint that what’s he’s really concerned with is passing from whole numbers to rationals and reals (but not complex). “4 baskets of 8 apples each” is still a discrete approach. I think
    that’s crucial, and I think the “baskets” approach therefore fails the Devlin Test. But I could be wrong.

    Only Devlin can say for sure.

    Reply

90. Jon says (interpreting Devlin):

    “we shouldn’t teach anything to students which contradicts ‘the way things really are’, by which he means the axiomatic presentation of fields, integral domains, and so on.”

    I agree that seems to be what he is saying, but its just still so wrong in so many ways, and it’s not just “limited” but wrong.

    For one, defining multiplication in the usual “traditional” way on whole numbers and extending to rationals and then to reals does not contradict any modern theories. Its just a different development. If there were any true contradiction between the traditional and some modern approach then so much the worse for the modern approach.

    Secondly, Godel showed that “the way things really are” and axiomatic developments (for anything as complex as number theory) are *not* the same.

    Thirdly, most mathematicians would agree that the modern theories do not make traditional approaches “totally and utterly false”.

    Reply

91. While musing on the notion of function equality, I do now recall Devlin saying something about the processes are different.

    To quote again:
    “Riding my bicycle gets me to my office in about the same time as taking my car, but the two processes are very different.”

    Now that’s a peculiar notion to come from a mathematician.

    While the very word “function” seems to denote action, or doing, the modern concept of a function is as a set of pairs, pairs whose first element comes from the domain and the second from the range. In this view, what defines a function is just the pairing of the domain elements and the elements drawn from the range.

    Not “how” you got from here to there, to paraphrase Devlin.

    Reply

92. Jon,

    Does Lakoff deal with Godel in his book?

    Reply

93. Joe,

    The notion of “per unit” can extend to rational numbers. You can have “1.8 pounds for 1 yard” etc. And, as long as the “unit” is a unit for a continuous quantity, then the multiplier can become a rational number, too – If 1 yard of an iron pipe weighs 1.8 pounds, how much would 3 1/3 yard of the same pipe weigh?

    Some might say we have moved from an “equal group” to a “rate” metaphor, but this expansion (extension?) is an inclusive one in that we are not denying what we have previously done.

    To me, understanding of 8 as 8 “apples per basket” is a central idea of multiplication, and even though that may not be the most important idea at the time of the introduction at Grade 2/3, I think we should be careful about how we present the idea of multiplication to children. I think the idea of “equal groups” is simple enough for children that we don’t need to provide additional metaphor – which can be misunderstood.

    Reply

94. Joe,

    Lakoff is mostly concerned with showing how the development of mathematics is intimately connected with the way we, as humans, perceive the world, through the use of layers of increasingly more complex ‘metaphor’s. One theme of the book is that we can reject the Platonic interpretation of maths as being ‘really out there’ without dissolving into post-modernist waffle about all truth being relative.

    Godel’s work is mentioned (pause as I flick through the index) twice in the book. First, in connection with the continuum hypothesis, along with Cohen: “””From the perspective of our mathematical idea analysis, this means that whether or not the Continuum hypothesis is ‘true’ depends on the underlying conceptual metaphors characterising the concept ‘set’.””” And then later, in passing, when talking about computability.

    A connected quote, from page 352 of the book:
    “””There is no such thing as ‘the’ geometry or ‘the’ set theory or ‘the’ formal logic. Rather, there are mutually inconsistent versions of geometry, set theory, logic, and so on. Each version forms a distinct and internally consistent subject matter.“””

    But enough shilling for a book :).

    Reply

95. Well, Godel was known as a Platonist which is why I ask. And he was concerned with whether the CH was true. The book sounds interesting, though I doubt it sounds the death knell for Platonism and its kin. It could be that math is both eternal and impersonal yet perceived by humans in innately human ways. I might have to read it, just to see how he deals with the “unreasonable efficiency of mathematics in describing the natural world” to quote some famous physicist or so-and-so.

    Reply

96. Tad – I understand. I think “copies of” can also extend to rationals.

    And the way you put it:

    “this expansion (extension?) is an inclusive one in that we are not denying what we have previously done.”

    — is very nicely put. That is what the traditional approach (that Devlin says is “false”) is all about.

    You are “preaching to the choir” as they say, if you are trying to convince me.

    Reply

97. My blushes, Mr. Ingram! Thanks for the very articulate comment on my blog. There’s a lot of conversation about this topic on two lists: mathtalk@yahoogroups.com, which I moderate, and etawm@googlegroups.com . Tad Watanabe is a participant on both lists, as am I. This whole issue has really promoted conversation in lots of places. I’ve gotten three interesting posts from Prof. Devlin, gracious and complimentary, and in the last one, a definite attempt to answer requests for a solid example of multiplication as something that can’t be viewed as “repeated addition” that would make sense to K-5 teachers and K-5 students. I’m thinking about all this quite a lot when I have time. I remain very much in agreement with what Mr, Ingram and some others here are saying. I’m also a Lakoff and Nunez fan, despite some errors (many of which were corrected but then somehow butchered by the printer in the second printing: see comments on their web page .

    Hope folks here will feel free to join the two lists mentioned above. I’ll be steering readers there here again, as I did on my blog. Intriguingly, an outspoken opponent of public education and what I speak of favorably as progressive mathematics education teaching and reform, claims repeatedly on yet another list, the volatile math-teach@mathforum.org, that “there are no open questions in mathematics pedagogy.” If I’ve ever seen strong proof of how wrong that statement is, the conversations that have popped up in response to the Devlin pieces are it.

    Reply

98. For the very interested (in aximomatics etc.) here is a very nice essay sure to rock somebodies boat:
    (Scroll down to page 155 – the essay entitled “Wings not Foundations!” )

    http://books.google.com/books?id=FYhKd9RVGQ0C&pg=PA242&lpg=PA242&dq=godel+and+ch&source=web&ots=3UtMMXMwr1&sig=MvhrAHWQG21VDmARKQWw5T3-A8c&hl=en&sa=X&oi=book_result&resnum=1&ct=result#PPA157,M1

    Reply

99. Is Devlin being inconsistent in his bias against the principle of harmless fallacy by picking on K8 math ed?

    What, is the purpose of those Real Analysis classes, if not to disabuse students of the fallacies and bad habits engendered by a heuristic approach to Calculus which is taught by university mathematicians ? What’s that snarky saying that I occassionally hear bantered about, “Analysis is Calculus taught correctly.” He says it’s okay to slop up the understanding of the complex numbers…until they hit which math course?

    PS I was another person who instantly thought of Peano when he said that the operations of basic arithemetic couldn’t be derived.

    Reply

100. Argh! Devlin! Niederberger is right.

     How can anything that includes the distributive law not be repeated addition? Define two operators @ and ^ and a set of elements S={a,b,c,…}. Suppose (S, @, ^) is field where a@(b^c) = a@b^a@c, then isn’t @ going to be repeated ^? Let e be the @ identity element. That is, e@x=x and o^x=x for all x in S. Then a@(e^e)=a@(e^e)=(a^e)^(a^e)=a^a. It at least has to contain the idea of repeated addition no matter how we use some sort of so called “empty” formalism to construct S in the first place.

     But even beyond that, real analysis/calculus is/are just the limiting cases of what derives entirely from this repeated addition concept. So, saying that something like pi*pi isn’t really repeated addition isn’t really true like what Devlin is saying. It is true that it isn’t *just* repeated addition, but I am not sure how we would really know what it is *without* repeated addition. What it “really” is is a limiting case of a sequence of rational numbers each term of which is arrived at based ultimately on various repeated additions! The complex numbers are just the real numbers adjoin a special new element i where i*i=-1.

     I’m not necessarily bound to Peano’s Axioms, here. I’m open to some new set of ground breaking axioms, even. But, any such set of axioms has to go through the distributive law at some point. At that point, it is at least going to have to include the idea of repeated addition. But, truthfully, we are going to have to go through it at one point or another in a really elementary fashion when nothing else is going on but the distributive law and that is when it will include repeated addition and nothing more than repeated addition. That is to say, in any derivation of any of this, I think you will always have to have it come back in some profound way to repeated addition and extensions thereof as opposed to some other completely different alternative.

     (And, by the way, nothing I am doing here is some sort of “empty formalism”. I’m talking about abstract algebra and real analysis. There are no bigger fields for rank-and-file mathematics. Unless you consider all of mathematics to be an “empty formalism”, you have to address this. And, also this is NOT a pedagogical matter but a mathematical one.)

     Reply

101. I should clarify that I don’t mean “just adding the distributive law” exactly. I mean constructing a field “from scratch” that has the distributive law as opposed to extending the set of a field to another larger set as well as the field operations to make sense on that larger set so that you have a larger field in the end that contains the original field. You can “just add the distributive law” to a group by defining multiplication in a way that distributes over the group operation and not even make it to being a field. For instance: the ring of nxn matrices for which I would be hard pressed to interpret matrix multiplication as iterative addition. Nevertheless, though, it does contain the concept of iterative addition since if A is an nxn matrix and I is the nxn identity matrix, A(I+I)=A+A.

     Also, I’m guessing there might be a field or integral domain out there which is not generated by its multiplicative identity and the additive inverse of the multiplicative identity. Finite fields are cyclic. But, perhaps there is some infinite field that is a counterexample to all of this in which multiplication is not exactly iterative addition, perhaps, because of the fact that it is not so generated. At any rate, all of that is very far a field of the reals or the complex numbers and multiplication of actual *numbers*.

     Reply

102. Argh! Of course, there are infinite fields that are not *generated* that way. But, if you made it this far, you know what I mean by now….

     Reply

103. Does anyone feel nostalgic for that old song from Lamb Chop’s Play-Along: “This is the song that doesn’t end…”

     Wow! It has been fun to watch this discussion flow, even though I freely admit that some of it has gone over my head. (I’ve admitted before that my retention of college-level mathematics is poor.)

     For anyone who is still trying to keep up with the discussion, here are a few new blog posts:

     Devlin’s Right Angle, Part III
     Devlin’s Right Angle, Part IV
     Devlin’s Right Angle, Part V
     The article that launched a thousand posts…

     Reply

104. Well, it’s nice people are writing about me (blush 😉

     Here’s my challenge though- for whole numbers only – show me that Peano’s definition of multiplication via recursive addition is “totally and utterly false” as Devlin has stated. Use a supercomputer if desired.

     That’s it –

     Now,to Text-Savvy, as to the equation a+a+a+a = 6 — considered as a Diophantine equation it has no solution. If you need more help please ask directly. LOL!!!

     Reply

105. Oh, and by the way, I have it from Devlin directly (email) that

     ” sorry, mathematics is not a matter of opinons,
     it’s either right or wrong. and multiplication
     is not repeated addition on any domain.”

     So – there it is – Devlin is saying:

     1. On ANY domain (say, pairs of non-negative integers) that repeated addition (meaning the usual and common definition given in schools, or the absolutely equivalent formulation by Peano) is NOT multiplication –

     and

     2. He’s talking mathematically (he says he’s not taking philosophically, not pedagogically, not guru-in-the-sky-new-age.)

     So – show me that on the domain of pairs of non-negative integers either the usual classroom definition as repeated multiplication (use wikipedia for a neutral party definition!) or Peano’s definition is “totally and utterly false”.

     Please make it a mathematical proof – not a sidestep, a semantic quibble, an appeal to some authority, or a stamp-the-foot insistence.

     Reply

106. And, at the risk of being utterly and totally clear on my position, and as has been said before, when I say “A” *is* “B” – where “A” and “B” are functions on some domain, I mean precisely what the usual definition for function equality states – that for every element of the domain the functions “A” and “B” have the same functional values. All this was put plainly to Devlin before he made the assertion that:
     no – they are *not* the same function.

     So substitute for “A” the usual old definition via repeated addition, and for “B” the “multiplication” that Devlin is talking about, and the domain here is given as non-negative integers.

     Prove them not the same.

     Reply

107. “Please make it a mathematical proof – not a sidestep, a semantic quibble, an appeal to some authority, or a stamp-the-foot insistence.”

     I’m with you on this one Joe. Right now all we’ve got is proof by repeated assertion.

     Can we forward this to Good Math/Bad Math?

     Reply

108. “However, the multiplication of any two integers *can* always be reduced (or thought of, or defined by) repeated addition.”

     And yet, when you take it upon yourself to reduce or think of or define 4a = 6 into/as a + a + a + a = 6, you can’t solve it.

     My seven-year-old can solve it.

     Even some bright Kindergarteners I know can solve it.

     So, why can’t you solve it? (By the way, the solution is a = 1.5; if you can’t figure that out, then trust me, I won’t be turning to you for any math questions.)

     I’m sure you’re still wrong as to the definition of multiplication as repeated addition. But, given this example, even if you were right, why would you want to be?

     Reply

109. I don’t think that’s what Joe said. Limited to the integers (as a Diophantine puzzle), the equation has no solution.

     But of course, when rational numbers are allowed, it can be solved. It can even be done by a student whose only understanding of multiplication was repeated addition — as my own son did (to my surprise) with a similar puzzle when he was 5yo.

     4a = a + a + a + a = 6 ?
     1 + 1 + 1 + 1 is too small.
     2 + 2 + 2 + 2 is too big.
     1.5 would be any student’s next guess, and it works.

     I’m not arguing that “repeated addition” makes a good definition for multiplication, because I agree with Joshua and Devlin that it doesn’t. But it certainly can be used as a substitute procedure in simple problems.

     Reply

110. But, 1.5 is nothing more than the number which when added to itself equals 3. Or, equivalently, it is the multiplicative identity added to itself 3 times multiplied by the multiplicative inverse of a number equal to the multiplicative identity added to itself twice. So, don’t act like you have come up with something new, here, that is not repeated addition. To use nothing but the repeated addition concept to solve it…

     (a+a)+(a+a) = 6
     b+b = 3+3
     b=3

     or a+a=3

     a is that number which when added to itself equals 3 which you simply have to define into existence and call “1.5”.

     Reply

111. I did mention in my post that no guessing was allowed, and both attempts thus far have involved guessing.

     And, I suppose you’ll have to catch me up on the terminology, but even if you classified the equation as the Snuffleupagus equation, it’s STILL unsolvable with only repeated addition in your toolkit.

     You simply can’t escape the fact that multiplication and repeated addition are different operations. That they get the same results in the natural numbers is not at issue.

     The point I’m trying to make is that EVEN IF you’re right about the idea that multiplication basically bottom-lines out to be repeated addition, the fact that the definitional power that comes with that doesn’t even allow you to solve what should be a simple one-step algebraic equation without resorting to guessing, then isn’t it pretty much useless?

     Reply

112. I am curious about Ted Watanabe’s comment about explaining addition as requiring the same units (apples plus apples) whereas multiplication may involve different units (apples per basket times number of baskets).
     If I were to make this statement in the classroom, I wonder how I would address a task such as, “A basket contains 3 apples, 4 oranges and 10 walnuts. How many items are in the basket?” These items are not of the same type, and yet they may still be added.

     Reply

113. Isn’t 3/7 x 14 repeated addition if you break it into 2 steps? 3×14 = 42 (that’s the repeated addition everyone agrees on, 14 + 14 + 14). Then you have a division problem of 42/7, and your answer is 6. Is there anything wrong with teaching fraction multiplication as repeated addition if we break it down like this?

     PSU MthEd497A represent!

     Reply

114. I think the problem here is that we are teaching multiplication to children at a young age. Most of us learned our multiplication tables at the age of 7 or 8. How else are you supposed to explain to children at this age exactly what multiplication is? I believe this issue is just like everything else in mathematics; when you first learn a concept, you learn the basics and as you grow older and learn more in depth, you realize the full concept of the subject matter.

     Reply

115. I really liked the idea of AND for addition, and OF for multiplication. However, i do not see any other way to explain multiplication than as repeated addition.

     If we look at the problem 8 x 3 we can explain it as 8 of the unit 3 which is easy to comprehend but when we write it out we get 3 3 3 3 3 3 3 3.

     But how do we explain how to combine them other than to just add them up, which is just like repeated addition. So does anyone have a better way to answer my question?

     Reply

116. When it comes to learning multiplication, how can we provide no transition from addition? Multiplication can be a very difficult concept to learn, especially when we just deal with grouping. If we use addition to set a foundation, multiplication becomes much easier for students to understand in terms they already know. If we start out by saying, ” how many blocks we have?” then we can continue into “how many groups can we make out of this number of blocks?” It then becomes easy to see that two groups of eight make sixteen, but four groups of four also make 16. This method is useful for the transition. Later when students have a firm grasp of multiplication use larger numbers that they can’t use repeated addition to solve. This method makes math more connected.

     Reply

117. Although I believe that multiplication and addition are different processes, using one to build upon the other may help students to see their connection to each other. Teaching multiplication without mentioning addition makes it difficult for students to connect one process to other. Perhaps, teachers can provide students with activities that show the advantages of using one over the other; multiplication provides a much faster answer, whereas in addition, counting takes more time and is less efficient.

     In addition, I do not think teachers can tell students that finding certain answers are not possible. For example, “you can’t subtract a larger number from a smaller number” convinces students that there is no situation in which that occurs. Yet, farther into the math program, they learn it is possible, and it is called a negative number.

     Telling students that they can not use certain processes to find answers may cause more confusion than expected. Instead of saying “no” teachers can provide students with some type of connection to their prior knowledge and accentuate their similarities and differences, as well as advantages and disadvantages. This way, students can obtain a deeper understanding of why and how they “do” math.

     Reply

118. I’ll admit I haven’t read all the comments here, but I’d like to offer something. Perhaps multiplication of non-integers can be understood by students as the result of traveling at some speed. If you travel at speed v for a time t, the distance traveled is vt.

     This has the glaring flaw that it’s not symmetric in interchanging v and t, though; you can’t immediately see that vt = tv.

     Reply

119. I will add one thing to the above discussion that I don’t think I said here. Actually, there is at least one way to do this so that multiplication doesn’t reduce to repeated addition and that is the synthetic geometry way. Actually, that is plenty rigorous and for that matter Euclid is plenty rigorous. Just because he had a few holes doesn’t mean he was like Newtons calculus or something. (Good lord! I bet most actual papers submitted for publication in professional joirnals have more holes.) He was almost entirely rigorous and correct. But, to fill in those holes, you can use Hilbert’s (or better yet, Tarski’s first order) axioms for synthetic geometry. And, that will be perfectly rigorous. And, then you could do “geometric arithmetic” just as it is presented in the Elements (which is fine as far as I know) so that multiplication would “really” be area (probably) and not repeated addition. Of course, it would still be possible to show that multiplication can be accomplished with repeated addition, but the original basis for understanding it in that case would be as area. I just wanted to make sure that we all know that synthetic geometry is not inherently flawed or unrigorous (or, for that matter, that Euclid is not just all jacked up six ways from Sunday, either).

     But, the reason that doesn’t really matter is because we don’t actually do math that way. We all do analytic geometry in virtually every context math is done in except for specifically teaching synthetic geometry. So, unless you are calling for a rewrite of modern mathematics, then you cannot really resort to such an argument.

     Reply

120. Jon mentioned Euclid earlier and encouraged me to pull this off the back burner and publish it:

     Euclid’s Geometric Algebra

     Reply

121. Denise,

     I think that ultimately Euclidean geometry were inadequate for a rigorous development of the real numbers. I wish I could add more thoughts on to that right now but I’ve only made it into the first 20 pages of Dedekind’s Theory of Numbers. He just couldn’t use Euclid to do everything that needed to be done…so he says.

     Reply

122. From a set-theoretic perspective, it seems to me that the two operations coincide. If f and g are functions from R to R where f(x)=nx and g(x)=x+x…+x n times, then the functions have the same domain and codomain and value on arbitrary elements.

     Reply

123. Nm, I just realized the above only works for integer values of n.

     Reply

124. I think it’s funny that this debate has boxed the multiplication-is-really-repeated-addition folks into such a corner that they have to stretch out to Diophantine equations, synthetic geometry, set-theoretic, Hilbert?, Tarski?, and Euclid.

     It’s simple multiplication, for crying out loud!

     If you need a Master’s degree in mathematics to make repeated addition work . . . sheesh. Hilarious!

     Reply

125. Joshua – answer the challenge. You are trying proof by ridicule – that’s editorializing, not math. You are the boxed-in one, grasshopper.

     Reply

126. “You simply can’t escape the fact that multiplication and repeated addition are different operations. That they get the same results in the natural numbers is not at issue.”

     (I hear foot-stamping when I read this!)

     Oh, contraire, but it *is* at issue. “The same results” (i.e., identical functional values; f(x) = f(y) for all x,y in the functions domain) – that’s how mathematicians have been defining function equality for some time now. Devlin and you apparently want to define mathematical functions by their “processes” whatever *that* means — completely non-standard, and you will have a hard time recruiting mathematicians into this process-oriented view.

     ————–

     Speaking of which – although the definition of function equality is completely insensitive to *how* (by which process) functional values are computed (indeed- whether they are even computable in theory) I totally missed how Devlin proposes to have students actually calculate the results of multiplying two numbers without using addition. Anyone know how offhand? Suitable for 2nd-3rd graders?

     Reply

127. Adrian – re: your comment on geometry – point well made. I must admit I can see now how one could totally avoid addition if one were willing to go to lengths. Even so, it would be a roughly equivalent (speaking informally of course) approach, not one which negates the validity of the other(s).

     Reply

128. Boy I hope someone caught the pun in my last post 😉

     Reply

129. Denise says:
     “But of course, when rational numbers are allowed, it can be solved. It can even be done by a student whose only understanding of multiplication was repeated addition — as my own son did (to my surprise) with a similar puzzle when he was 5yo.”

     Frankly, I’m of the opinion that any multiplication between rational numbers can be fairly easily understood as repeated-addition of fractional parts (the size, of course, depending on the multiplicands – 3/2 x 4/3 can be understood as the repeated addition of 12 “pieces” each of which is 1/6, or alternatively, as repeated-addition of 1 copy of 4/3, plus another half-copy of 4/3, if you can follow that without me drawing the appropriate pictures!)

     Disclaimer – I’m not claiming that’s the *best* way, just a way that works.

     Reply

130. Your challenge is baloney, Joe. And you should know it. You’re still arguing about the procedural connection between the operations.

     But, whatever, slick. I’m your huckleberry.

     Consider two functions: (A) y = 2x and (B) y = 2((sqrt(x^2)/4.5) x (1.5 x 3)).

     So long as I didn’t make a mistake there, I did as Joe specified: “for every element of the domain the functions ‘A’ and ‘B’ have the same functional values.”

     Everyone who is reading this can see that those two functions output the same “functional values.” That is, if you were to graph them, they would be the same line (or the same ray, since we can’t go outside of the first quadrant).

     What everyone who is reading this may NOT know, however, is that, according to Joe’s logic, the operation of square-rooting a number is now part of the definition of multiplication.

     The only thing he seemed to care about was that the two “functions” (repeated addition really isn’t a function) found the same output, given the same input, every time. Therefore, repeated addition must be the same as multiplication.

     Similarly, I have shown that square-rooting a number is just as legitimate in helping to create a function that outputs equivalent values. Therefore, radicals should be part of our definition of multiplication.

     Joe is arguing for the equality of repeated addition and multiplication on precisely the same premise. Since the two functions create the same ray in the first quadrant, they are the same. And, so, since we used a radical in our equivalent expression, that operation must play a part.

     Obviously, that’s bullshit. Q.E.D.

     I’m still waiting for someone to step up and show the all-powerful mathematical force that is repeated-addition-as-multiplication which can solve one-step algebraic equations.

     Reply

131. Synthetic geometry, Hilbert and Tarski is what it takes for YOU to be right, Fisher, not us. That is what it would take to make multiplication NOT repeated addition. I have answered your challenge to use repeated addition to solve your little equation. Now answer the challenges that have been put before YOU and even actually DEFINE “1.5” WITHOUT repeated addition. Or, better yet, admit defeat (at least to yourself) and have the dignity to bow out. Stop trying to call bullshit on something that has been more than amply demonstrated by now.

     The only person reaching here is you. If you step it up and start even more aggressively calling bullshit, you will only provoke someone.

     Reply

132. “The only thing he seemed to care about was that the two “functions” (repeated addition really isn’t a function) found the same output, given the same input, every time.”

     Yes sir – that’s the standard definition of functional equality. Given f:D->R & g:D->R, then f = g iff. f(a) = g(a) for each a element of D.

     Now please kindly tell (without the naughty language) what your definition is.

     Please also tell us why repeated addition is “not really” a function.

     (Sounds of more foot-stamping and cursing -oooh!)

     Reply

133. Sorry – my end-bold tag got munged past the last “your”.

     [Edited to fix that for you. —Denise]

     Reply

134. Sorry, pumpkin.

     Your reasoning is “bullsnot.” How’s that?

     And, nope, no more help for you. I’m not going to waste my time teaching you math in this thread.

     Reply

135. Joshua – psst! “sqrt” for sure is not really a function, and your little identity doesn’t hold because “sqrt” is not uniquely defined!

     Reply

136. LOL ROTF!!!!

     Reply

137. And yet, by your logic, it should belong to the definition of multiplication!

     Good stuff.

     Reply

138. *Sigh*

     There’s a reason why I called it a FUNCTION.

     Next.

     Reply

139. Have yourself a refresher course for free:
     http://plato.stanford.edu/entries/set-theory/primer.html#3

     quoting:
     ” The Axiom of Extensionality can be applied to functions as follows.
     Lemma. Let F and G be functions. F = G if and only if dom F = dom G and F(x) = G(x) for all x ∈ dom F. ”

     You think I made it up? LOL!

     Reply

140. Okay, guys, I’m calling a halt to this. It’s been fun, but I think we can agree that neither side is going to convince the other.

     I have rescued a few comment posts that were wrongly tagged as spam by Akismet. Everyone has put out his best arguments, and reasonable readers can make up their own minds. If we take this much farther, the only place to go will be to descend into name-calling.

     I am closing comments on this thread.

     [Oh, bother! When I closed comments, all the old ones disappeared. I had to allow comments again to let them show — but please, no more arguing. Okay?]

     Edited to add: The conversation continues, however, over at Good Math, Bad Math:

     Teaching Multiplication: Is it repeated addition?

     Check it out!

     Reply
141. Pingback: Multiplication? Addition? Comments? « JD2718
142. Pingback: Once more on Devlin (but not on teaching) « JD2718
143. Pingback: The “Multiplication is Not Repeated Addition” Research « The Number Warrior
144. Pingback: Devlin (repost) « JD2718
145. Pingback: Multiplication as Scaling with a Multiplying Menace – Math Book Magic

146. Thank you for this post! I teach struggling math learners and they are often confused by the idea that multiplication is repeated addition and it is also not addition. They are even more confused by exponentiation is repeated multiplication but not addition and also not multiplication. I used the idea that exponentiation is a doubling or a tripling or a quadrupling or a … and so on. So 3^4 is a tripling that is done 4 times. And it was magical! Astonishingly well received by struggling math learners. It was actually easier for them to think of exponentiation as something different from multiplication. THANK you for your blog!

     Reply

     1. That’s a great way to think about exponentiation. Kids can relate to it in a pictorial or hands-on way with staircases (on graph paper or with blocks). This blog post calls them “Cuisenaire Rod Staircases That Count Times-N.” http://www.arithmophobianomore.com/cuisenaire-rod-staircases-counting-counting/

        And even better: This provides a natural, intuitive meaning for logarithms. The log of a number is asking “Which step in the staircase is that number?”

        Reply

147. Wow, I’m very late to this party, but I have to say “Mutliplication ain’t no repeated addition” is exactly right. It’s a double-negative that nullifies itself to the equivalent statement, “Multiplication is repeated addition.” I appeal back to the New Math injection of some sensible (but not overdone, as if often was back in the day) set theory into the mix. When talking about natural and whole numbers (and even integers for that matter), this is absolutely correct. It is repeated addition, which then leads to additional interpretations. Those interpretations become necessary as our number system expands, and there no “lie” in that. Domains are important. When domains change, new things happen.

     Reply

148. Hello, Denise! I was enthusiastic starting reading this post, but then I discovered the drawing you proposed for illustrating the multipliation still looks like repeated addition of units : /

     Reply

     1. Yes, it does. Except that the “unit” can be any size, and we can have any quantity of them.

        Scaling can also be done with a double number line — which probably works better — but that went beyond my artistic abilities to draw. It would need to be an interactive thing.

        I’m mostly interested in changing the way we teachers *talk* about multiplication. Look at my follow-up post for more thoughts.

        Reply

149. For what it is worth (many years later), when I taught middle school (also many years ago), I made a multiplication machine out of a 1×4, an elastic band, and a heavy duty stapler.

     I marked a zero near the middle of the board, then marked and labeled units at 2 inch increments. I also put marks on the board for multiples of 1/12 (which gave me half integers, thirds, fourths, and sixths). I stapled one end of the elastic to the zero, and left the other end loose (I trimmed it so that it reached to the end of the board). I then stretched the elastic to about half of its total stretchiness, temporarily pinned it, and marked off the integers on the elastic so that they lined up with the board.

     To multiply a*b, stretch the elastic so that the 1 on the elastic aligns with a on the board. Find b on the elastic—the corresponding number on the board is a*b.

     Reply

     1. Cool! That’s a great way to demonstrate multiplication as scaling.

        The old slide rules used to do something similar, but not as intuitive because they were based on logarithms (so they didn’t have to be stretchy).

        Reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.