As I said in an earlier post, we don’t want to give our children a method because that acts as a crutch to keep them from making sense of math.
But what if our children get stumped on a tough fraction calculation like 1 1/2 ÷ 3/8?

As I said in an earlier post, we don’t want to give our children a method because that acts as a crutch to keep them from making sense of math.
But what if our children get stumped on a tough fraction calculation like 1 1/2 ÷ 3/8?

This game helps students master multiplying and dividing fractions.
Many parents remember struggling to learn math. We hope to provide a better experience for our children. And one of the best ways for children to enjoy learning is through hands-on play.
So what are you waiting for? Let’s play some math!
Math Concepts: multiplying fractions, equivalent fractions.
Players: two, or two teams.
Equipment: printed game board, colored markers or a set of matching tokens for each player, two glass gemstones or other small tokens to mark the factors.

I just discovered a fascinating fact: In some places in the world, mixed numbers apparently don’t exist.
So that made me curious about my blog readers:
And if you DO know mixed numbers, can you simplify this mess:
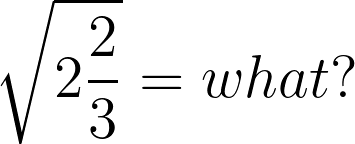
[If you enjoy dry math humor, the answer is worth the work.]

The all-time most-visited page on this site is my post about Math War: The Game That Is Worth 1,000 Worksheets. It’s easy to adapt to almost any math topic, simple to learn, and quick to play. My homeschool co-op students love it.
But Math War isn’t just for elementary kids. Several teachers have shared special card decks to help middle and high school students practice math by playing games.
Take a look at the links below for games from prealgebra to high school trig. And try the Math War Trumps variation at the end of the post to boost your children’s strategic-thinking potential.
Have fun playing math with your kids!

This week, I’m working on graphics for my upcoming book 70+ Things to Do with a Hundred Chart. I had fun with this complex fraction image.
It looks a bit cluttered. Possible tweak: Remove the brackets and instead use a thicker dividing line to show the thirds.
While I’m thinking about that, would you like a sneak peek at an activity from the book?
You don’t need a set of worksheets or lesson plans to learn math. All you need is an inquiring mind and something interesting to think about.
Play. Discuss. Notice. Wonder.
Enjoy.
Here’s how you can play complex fractions with your kids…
Print a few blank 120 charts and turn them sideways, so each chart has ten rows with twelve squares in each row.
Cut out the rows to make fraction strips with twelve squares on each strip.
Color a different set of squares on each strip. On some strips, arrange the colored squares all together at one end. On other strips, mix them around.
If we count each strip as one whole thing, what fraction of its squares are colored?
Match the strips that represent the same fraction.
On some of the strips, there will be more than one way to name the fraction. For example, if six squares are colored, we can call that 6/12 or 2/4 or 1/2 of the strip. These alternate names are easiest to see when the colored squares are all at one end of the strip, because you can fold the strip to show the halves or fourths.
How many different fraction names can you find for each set of colored squares?
We could also call the strip with six colored squares “1 1/2 thirds” of the whole strip. Can you show by folding why that name makes sense?
Or we could call the strip with five colored squares “2 1/2 sixths.”
When we have a fraction within a fraction like this, we call it a complex fraction, because it is more complicated than a common (or simple) fraction.
Another way to say it: Complex fractions have other fractions inside them.
A complex fraction is like a puzzle, challenging us to find its secret identity — the common fraction that names the same amount of stuff.
For example, how much is 3 1/3 fourths? One fourth would be three of the twelve squares on a fraction strip. So three fourths would be three sets of those three squares, or nine squares. Then we need to add one-third of the final fourth, which is one of the remaining three squares. So 3 1/3 fourths must be ten squares in all.
3 1/3 fourths = 10/12 = 5/6
How many complex fractions can you find in your set of fraction strips?
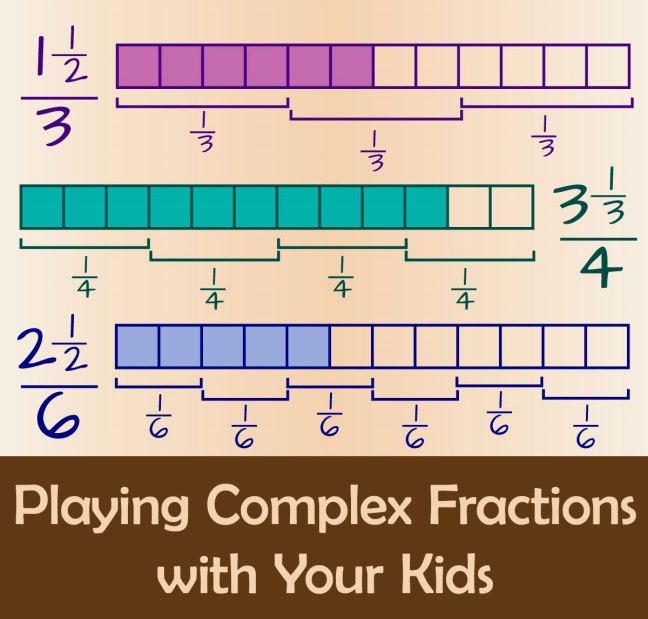
Can you figure out how much a one-and-a-halfth would be?
That is one piece, of such a size that it takes one and one-half pieces to make a complete fraction strip.
A one-and-a-halfth is a very useful fraction and was a favorite of the ancient Egyptian scribes, who used it to solve all sorts of practical math problems.
How about a one-and-a-thirdth? How many of those pieces make a whole strip? What common fraction names the same amount of stuff?
Or how much would a two-thirdth be? In that case, it only takes two-thirds of a piece to make a complete strip. So the whole piece must be greater than one. A two-thirdth’s secret identity is a mixed number. Can you unmask it?
Make up some challenge fraction mysteries of your own.

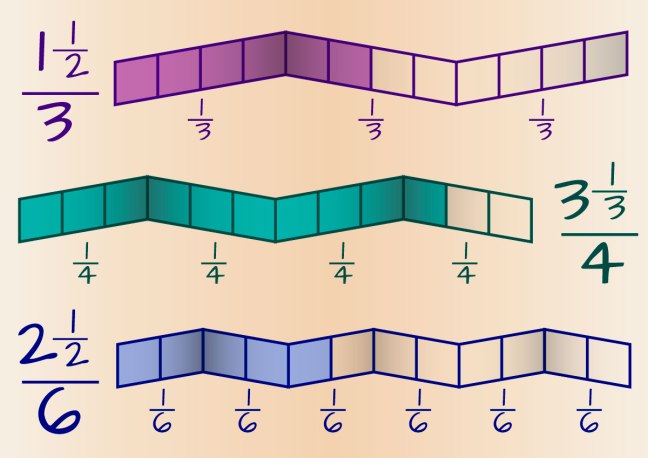
I’m still working on the graphics for my hundred chart book. Here’s the latest version of the complex fraction strips.
I like this one much better.
What do you think?
CREDITS: The slogan “Make Math Your Own” comes from Maria Droujkova, founder and director of the Natural Math website. Maria likes to say: “Make math your own, to make your own math!”
70+ Things to Do with a Hundred Chart is now available from Tabletop Academy Press.


I’ve been working on my next Playful Math Singles book, based on the popular Things to Do with a Hundred Chart post.
My hundred chart list began many years ago as seven ideas for playing with numbers. Over the years, it grew to its current 30+ activities.
Now, in preparing the new book, my list has become a monster. I’ve collected almost 70 ways to play with numbers, shapes, and logic from preschool to middle school. Just yesterday I added activities for fraction and decimal multiplication, and also tips for naming complex fractions. Wow!
Gonna have to edit that cover file…
In the “Advanced Patterns” chapter, I have a section on math debates. The point of a math debate isn’t that one answer is “right” while the other is “wrong.” You can choose either side of the question — the important thing is how well you support your argument.
Here’s activity #69 in the current book draft.
When you add fractions, you face a problem that most people never consider. Namely, you have to decide exactly what you are talking about.
For instance, what is one-tenth plus one-tenth?

Well, you might say that:
of one hundred chart
+ of the same chart
= of that hundred chart
But, you might also say that:
of one chart
+ of another chart
= of the pair of charts
That is, you started off counting on two independent charts. But when you put them together, you ended up with a double chart. Two hundred squares in all. Which made each row in the final set worth of the whole pair of charts.
So what happens if you see this question on a math test:
+
= ?
If you write the answer “”, you know the teacher will mark it wrong.
Is that fair? Why, or why not?
CREDITS: Feature photo (above) by Thor/geishaboy500 via Flickr (CC BY 2.0). “One is one … or is it?” video by Christopher Danielson via TED-Ed. This math debate was suggested by Marilyn Burns’s blog post Can 1/3 + 1/3 = 2/6? It seemed so!

It’s here! My long-awaited upper-elementary Math You Can Play games book has finally hit the online bookstores.
Multiplication & Fractions features 25 kid-tested games, offering a variety of challenges for school-age students. Children master several math models that provide a sturdy foundation for understanding multiplication and fractions. The games feature times table facts and more advanced concepts such as division, fractions, decimals, and multistep mental math.
Click here to find Multiplication & Fractions at your favorite bookstore.
170 pages, ebook: $5.99, paperback: $17.99.
Maybe you never really understood what multiplication means or what fractions are? As long as you start with an open mind and are willing to engage playfully, the activities in the book can help you as you help your kids.
Anecdotally, these two areas are the first major stumbling point for students in their math studies. The sequencing in the book will help kids develop a strong foundation.
Kids (and parents!) find these games fun. I’ve been field testing math games for the last 18 months and keep seeing how engaged kids get when playing math games.— Joshua Greene
Multiplication & Fractions Math Games from Denise Gaskins (a review)
Chapters include:
If you are a parent, these games provide opportunities to enjoy quality time with your children. If you are a classroom teacher, use the games as warm-ups and learning center activities or for a relaxing review day at the end of a term. If you are a tutor or homeschooler, make games a regular feature in your lesson plans to build your students’ mental math skills.
So what are you waiting for? Clear off a table, grab a deck of cards, and let’s play some math!
It starts with models that are visual explanations of the concepts. Gaskins also breaks learning these concepts into comfortable steps that emphasize patterns and relationships, the real ideas that are behind properly understanding multiplication and fractions (indeed, math generally).
The sequence of games in each section starts by building familiarity and then fluency (speed) to solidify all of that work.— Joshua Greene
Multiplication & Fractions Math Games from Denise Gaskins (a review)
Most of the Math You Can Play games use materials you already have around the house, such as playing cards or dice. But this book introduces multiplication and fractions with several games using two special mathematical model card decks.
Click here to download the Multiplication & Fraction Printables, featuring all the math model cards, hundred charts, and game boards you will need for any game in the book.
Click to read the earlier posts in this series: Understanding Math, Part 1: A Cultural Problem; Understanding Math, Part 2: What Is Your Worldview?; Understanding Math, Part 3: Is There Really a Difference?; and Understanding Math, Part 4: Area of a Rectangle.
In this post, we consider the second of three math rules that most of us learned in middle school.

 Fractions confuse almost everybody. In fact, fractions probably cause more math phobia among children (and adults) than any other topic before algebra.
Fractions confuse almost everybody. In fact, fractions probably cause more math phobia among children (and adults) than any other topic before algebra.
Children begin learning fractions by coloring or cutting up paper shapes, and their intuition is shaped by experiences with food like sandwiches or pizza. But before long, the abstraction of written calculations looms up to swallow intuitive understanding.
Upper elementary and middle school classrooms devote many hours to working with fractions, and still students flounder. In desperation, parents and teachers resort to nonsensical mnemonic rhymes that just might stick in a child’s mind long enough to pass the test.

Do you remember our exploration of the area of a rectangular tabletop?
Now let’s zoom in on our rectangle. Imagine magnifying our virtual grid to show a close-up of a single square unit, such as the pan of brownies on our table. And we can imagine subdividing this square into smaller, fractional pieces. In this way, we can see that five-eighths of a square unit looks something like a pan of brownies cut into strips, with a few strips missing:

But what if we don’t even have that whole five-eighths of the pan? What if the kids came through the kitchen and snatched a few pieces, and now all we have is three-fourths of the five-eighths?

How much of the original pan of brownies do we have now? There are three rows with five pieces in each row, for a total of 3 × 5 = 15 pieces left — which is the numerator of our answer. And with pieces that size, it would take four rows with eight in each row (4 × 8 = 32) to fill the whole pan — which is our denominator, the number of pieces in the whole batch of brownies. So three-fourths of five-eighths is a small rectangle of single-serving pieces.


Notice that there was nothing special about the fractions 3/4 and 5/8, except that the numbers were small enough for easy illustration. We could imagine a similar pan-of-brownies approach to any fraction multiplication problem, though the final pieces might turn out to be crumbs.
Of course, children will not draw brownie-pan pictures for every fraction multiplication problem the rest of their lives. But they need to spend plenty of time thinking about what it means to take a fraction of a fraction and how that meaning controls the numbers in their calculation. They need to ask questions and to put things in their own words and wrestle with the concept until it makes sense to them. Only then will their understanding be strong enough to support future learning.
Click here to continue reading: Understanding Math Part 6, Algebraic Multiplication…
CREDITS: “School Discussion” photo (top) by Flashy Soup Can via Flicker (CC BY 2.0, text added).  This is the fifth post in my Understanding Math series, adapted from my book Let’s Play Math: How Families Can Learn Math Together—and Enjoy It, available at your favorite online book dealer.
This is the fifth post in my Understanding Math series, adapted from my book Let’s Play Math: How Families Can Learn Math Together—and Enjoy It, available at your favorite online book dealer.


My daughters didn’t want to admit to knowing me, when I stopped to take a picture of the sidewalk along a back street during our trip to Jeju. But aren’t those some wonderful fractions?
What do you see? What do you wonder?
Here is one of the relationships I noticed in the outer ring:

And this one’s a little trickier:
Can you find it in the picture?
Each square of the sidewalk is made from four smaller tiles, about 25 cm square, cut from lava rock. Some of the sidewalk tiles are cut from mostly-smooth rock, some bubbly, and some half-n-half.
I wonder how far we could go before we had to repeat a circle pattern?

[Feature photo is a screen shot from the video “the sausages sharing episode,” see below.]
How in the world can 1/5 be the same as 1/10? Or 1/80 be the same as one whole thing? Such nonsense!
No, not nonsense. This is real-world common sense from a couple of boys faced with a problem just inside the edge of their ability — a problem that stretches them, but that they successfully solve, with a bit of gentle help on vocabulary.
Here’s the problem:
Think for a moment about how you (or your child) might solve this puzzle, and then watch the video below.