Hobbit Math: Elementary Problem Solving 5th Grade

Posted on by Denise Gaskins

[Photo by OliBac. Visit OliBac’s photostream for more.]

The elementary grades 1-4 laid the foundations, the basics of arithmetic: addition, subtraction, multiplication, division, and fractions. In grade 5, students are expected to master most aspects of fraction math and begin working with the rest of the Math Monsters: decimals, ratios, and percents (all of which are specialized fractions).

Word problems grow ever more complex as well, and learning to explain (justify) multi-step solutions becomes a first step toward writing proofs.

This installment of my elementary problem solving series is based on the Singapore Primary Mathematics, Level 5A. For your reading pleasure, I have translated the problems into the world of J.R.R. Tolkien’s classic, The Hobbit.

UPDATE: Problems have been genericized to avoid copyright issues.

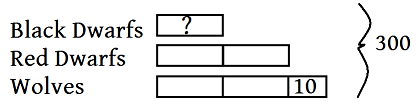
Continue reading Hobbit Math: Elementary Problem Solving 5th Grade

Narnia Math: Elementary Problem Solving 4th Grade

Posted on by Denise Gaskins

[Photo by armigeress.]

In 4th grade, math problems take a large step up on the difficulty scale. Students are more mature and can read and follow more complex stories. Multi-step word problems become the new norm, and proportional relationships (like “three times as many”) show up frequently. As the year progresses, fractions grow to be a dominant theme.

As a math teacher, one of my top goals is that my students learn to solve word problems. Arithmetic is (relatively) easy, but many children struggle in applying it to “real world” situations.

In previous posts, I introduced the problem-solving tools of word algebra and bar diagrams, either of which can help students organize the information in a word problem and translate it into a mathematical calculation. The earlier posts in this series are:

In this installment, I will continue to demonstrate the problem-solving tool of bar diagrams through a series of ten 4th grade problems based on the Singapore Primary Math series, level 4A. For your reading pleasure, I have translated the problems into the universe of a family-favorite story by C. S. Lewis, The Lion, the Witch and the Wardrobe.

UPDATE: Problems have been genericized to avoid copyright issues.

Continue reading Narnia Math: Elementary Problem Solving 4th Grade

Elementary Problem Solving: Review

Posted on by Denise Gaskins

[Bill Watterson identifies the trouble with math problems, through the eyes of Calvin and Hobbes.]

It’s time to revive and (hopefully!) finish my long-neglected series on solving word problems in elementary mathematics. I’ve been having fun making up the problems, so now I just have to write the posts. Coming up soon:

Since it has been more than two years since the last entry, however, I wanted to take a few minutes to recap our progress so far and to refer new readers back to the original posts:

Continue reading Elementary Problem Solving: Review

Solving Complex Story Problems II

Posted on by Denise Gaskins

[Oops! I found one more post from my old blog. It apparently slipped off the back of my metaphorical desk and has been sitting with the dust bunnies.]

Here is a math problem in honor of one of our family’s favorite movies…

Han Solo was doing some needed maintenance on the Millennium Falcon. He spent 3/5 of his money upgrading the hyperspace motivator. He spent 3/4 of the remainder to install a new blaster cannon. If he spent 450 credits altogether, how much money did he have left?

[Modified from a word problem in Singapore Primary Math 5B. Stop and think about how you would solve it before reading further.]

Continue reading Solving Complex Story Problems II

Ben Franklin Math: Elementary Problem Solving 3rd Grade

Posted on by Denise Gaskins

The ability to solve word problems ranks high on any math teacher’s list of goals. How can I teach my students to solve math problems? I must help them develop the ability to translate “real world” situations into mathematical language.

In two previous posts, I introduced the problem-solving tools algebra and bar diagrams. These tools help our students organize the information in a word problem and translate it into a mathematical calculation.

Working Math Problems with Poor Richard

This time I will demonstrate these problem-solving tools in action with a series of 3rd-grade problems based on the Singapore Primary Math series, level 3A. For your reading pleasure, I have translated the problems into the life of Ben Franklin, inspired by the biography Poor Richard by James Daugherty.

Continue reading Ben Franklin Math: Elementary Problem Solving 3rd Grade

Penguin Math: Elementary Problem Solving 2nd Grade

Posted on by Denise Gaskins

The ability to solve word problems ranks high on any math teacher’s list of goals. How can I teach my students to reason their way through math problems? I must help my students develop the ability to translate “real world” situations into mathematical language.

In a previous post, I analyzed two problem-solving tools we can teach our students: algebra and bar diagrams. These tools help our students organize the information in a word problem and translate it into a mathematical calculation.

Now I want to demonstrate these problem-solving tools in action with a series of 2nd grade problems, based on the Singapore Primary Math series, level 2A. For your reading pleasure, I have translated the problems into the universe of one of our family’s favorite read-aloud books, Mr. Popper’s Penguins.

UPDATE: Problems have been genericized to avoid copyright issues.

Continue reading Penguin Math: Elementary Problem Solving 2nd Grade

Elementary Problem Solving: The Tools

Posted on by Denise Gaskins

[This article begins a series rescued from my old blog. Moving has been a long process, but I’m finally unpacking the last cardboard box! To read the entire series, click here: elementary problem solving series.]

Most young students solve story problems by the flash of insight method: When they read the problem, they know almost instinctively how to solve it. This is fine for problems like:

There are 7 children. 2 of them are girls. How many boys are there?

As problems get more difficult, however, that flash of insight becomes less reliable, so we find our students staring blankly at their paper or out the window. They complain, “I don’t know what to do. It’s too hard!”

We need to give our students a tool that will help them when insight fails.

Continue reading Elementary Problem Solving: The Tools

Are You Smarter than a 3rd-6th Grader?

Posted on by Denise Gaskins

Here are a few challenging word problems from Singapore:

I did fine on the 3rd-grade problems, but I stumbled a bit on the 4/5th-grade “How much sugar…” problem. The toy cars were tricky, but manageable. I misread the problem with the chocolate and sweets at first — I think of chocolates as a sub-category of sweets, but in this problem they are totally different. (Perhaps “sweets” are what I would call “hard candy”?) Finally, I had to resort to algebra for the last two Grade 6 questions.

How many can you solve?

Solving Complex Story Problems

Posted on by Denise Gaskins

[Dragon photo above by monkeywingand treasure chest by Tom Praison via flickr.]

Solving-Complex-Story-Problems

Let’s play around with a middle-school/junior high word problem:

Cimorene spent an afternoon cleaning and organizing the dragon’s treasure. One fourth of the items she sorted was jewelry. 60% of the remainder were potions, and the rest were magic swords. If there were 48 magic swords, how many pieces of treasure did she sort in all?

[Problem set in the world of Patricia Wrede’s Enchanted Forest Chronicles. Modified from a story problem in Singapore Primary Math 6B. Think about how you would solve it before reading further.]

How can we teach our students to solve complex, multi-step story problems? Depending on how one counts, the above problem would take four or five steps to solve, and it is relatively easy for a Singapore math word problem. One might approach it with algebra, writing an equation like:

x - \left[\frac{1}{4}x + 0.6\left(\frac{3}{4} \right)x \right] = 48

…or something of that sort. But this problem is for students who have not learned algebra yet. Instead, Singapore math teaches students to draw pictures (called bar models or math models or bar diagrams) that make the solution appear almost like magic. It is a trick well worth learning, no matter what math program you use.

Continue reading Solving Complex Story Problems