Improper Fractions: A Mathematical Trauma

Posted on by Denise Gaskins

Feature photo (above) by Jimmie via flickr. Photo (right) by Old Shoe Woman via Flickr.

Nearing the end of Miquon Blue today, my youngest daughter encountered fractions greater than one. She collapsed on the floor of my bedroom in tears.

The worksheet started innocently enough:

\frac{1}{2} \times 8=\left[ \quad \right]

Those Frustrating Fractions

I wonder if that was a typo, because the next several questions followed a pattern that begged for a beginning:

\frac{2}{8} \times 8=\left[ \quad \right]

\frac{3}{8} \times 8=\left[ \quad \right]

\frac{4}{8} \times 8=\left[ \quad \right]

\frac{5}{8} \times 8=\left[ \quad \right]

\frac{8}{8} \times 8=\left[ \quad \right]

“Mom, I’m stuck!” she complained.

“Hmm. Those do look tricky. Could you do this one if it was 1/8?” I pointed at the 2/8 question, rewording it with our familiar translation. “Remember that the multiplication symbol means of. What would 1/8 of 8 be?”

She still looked puzzled. When she decides something is too difficult, she starts to build a mental brick wall, and it can take awhile to break it back down.

Back to the Basics

I pointed to the picture at the top of the page and reminded her how to make a fraction.

“If we took this bar and cut it into eight pieces, how big would one of the pieces be? What is 1/8 of 8?”

She thought for a moment. A few bricks tumbled. “One.”

“Good! And if 1/8 of 8 is one, then what would two of the pieces be? What is 2/8 of 8?”

The wall came down, letting in the light. She bowed her head over the worksheet, shielding it with her arm so I couldn’t watch her fill in the boxes.

It’s Too Much!

She worked happily until…

\frac{9}{8} \times 8=\left[ \quad \right]

\frac{16}{8} \times 8=\left[ \quad \right]

“I can’t do it!”

“What do you mean?”

She pointed at the fraction 9/8. “That’s impossible!”

“Well, if 1/8 is one, then how much would it be if you had nine of the pieces? You already figured out that 8/8 of 8 is eight, so lets put one more of the little pieces here.” I sketched a small square at the end of the rectangle labeled 8. “If we have one more piece, that would make 9/8, right?”

“It’s more than eight,” she said.

“That’s right. It’s more than eight. How much is it?”

“I can’t do more than eight. It’s too much!”

It was too much numerically, since the fractions were originally made (in her mind) by cutting a single bar into pieces. How could there be more pieces than the bar she had started with? It was too much emotionally, as well. She threw herself onto a pile of blankets and hid her face in the folds of cloth.

What’s in a Name?

“It’s okay to have fractions that are bigger than a whole thing, you know.” I tried my most encouraging voice. “If we had grilled cheese sandwiches for lunch, and we cut each sandwich in half, you could have three halves, couldn’t you?”

Whimper. Sniffle. No reply.

“You don’t like these fraction, do you? Somebody else who didn’t like this sort of fractions gave them their name. He called them improper fractions. Do you know what improper means?”

She looked up. “Not right?”

“You’ve got it! Fractions bigger than one just don’t seem right, do they? So he called them improper fractions, and that’s what we still call them today.”

A weak smile.

Happy Ending

I had mercy on her — after all, she is only in second grade. I told her she could skip all the fractions that were greater than one whole thing. She will have to learn how to work with improper fractions in a few years, but for now, I gave her my permission to ignore them. She happily scribbled over the questions and put her workbook away.

Still, she’s a bright girl, and somewhat stubborn. She is rarely content to leave a topic unconquered. The idea of improper fractions must have continued to simmer in her brain, because when I went back later to check the worksheet, I found that she had erased her scribbles and answered every question.

And they were all correct.

12 thoughts on “Improper Fractions: A Mathematical Trauma”

  1. Very cool. I love the explanation of “improper” fractions! I used to use Miquon with my older dc and loved it. I am thinking of revisiting it with my 5yo next year. It sure is a great program.

    Reply

  2. Wonderful that she got it and the explanation of “improper” is a good one. I think, though, that the problem is not with her. She was right! A fraction was defined as a part of a whole, and thus, 9/8 is not right. The book should have explained it to her and not jump it on her. It is an issue with many (pretty much all) books that assume kids can generalize at that abstract level, which is not true mostly, and improper (smile) at times.

    This is exactly why I explain it separately and in detail in my book. But you have my Fractions book, why not work with her with it?

    Reply

  3. Since it is not my level, I need to be careful, but I do think that:
    \frac{3}{8} = 3 \times \frac{1}{8} or
    \frac{3}{8} = 3 \centerdot (\frac{1}{8})
    needs to get worked in on the early side. It has to be useful sometime soon.

    Reply

  4. Denise–
    Following up on jd2718’s insightful comment, here are some other musings. Let me know if any of these might help your daughter… (sorry, no LaTeX noataion yet!)
    1. I wouldn’t ‘confound’ (Engelmann’s favorite term!) improper fractions with multiplying a fraction times a whole number just yet. You could first develop ‘improper’ using the standard ‘parts of ONE whole approach (the following is very well-known but read through it for the dialogue between parent and child and a few wrinkles):
    Lay out pizza (sorry, food always works for me!) cut up into 8 equal slices. Note the DI approach I seem to be using:
    “Ok, now show me ONE-EIGHTH of the pie. Good. Remember, whenever I ask for an eighth, you show me a slice. If I show you a slice, you say “One-eighth.” Ok, TWO-EIGHTHS. Good — 2 slices.”
    Show FIVE slices and ask for the fraction (important to go both ways to set the concept). Continue this standard fraction activity (which I’m sure you’ve done and she gets it easily) until you reach EIGHT-EIGHTHS. She should recognize of course that that’s one whole pie.
    NOW TAKE OUT A SECOND WHOLE PIE CUT UP INTO 8 = SLICES.
    “Show me NINE slices!” How many eighths would that be?
    So NINE-EIGHTHS IS the same as one whole pie and one slice: 1 + 1/8 etc…
    With a little more practice, she’ll start feeling comfortable with improper fractions but notice I did not choose to combine this conceptual understanding with multiplying 9/8 times 8. This should come later in my opinion.
    2. jd2718 is suggesting the importance of rewriting A/B as A times 1/B. This is a good way of moving to multiplication of a fraction by a whole since the child already has learned the meaning of A/B. However, I believe there are some conceptual rungs on the ladder to insert between 3/8 and three times one-eighth. Thus far I’m assuming your daughter has already developed an understanding of multiplication using a variety of models/contexts. Let’s see if she can apply rhis knowledge to multiplying with a fraction. Here’s one model of multiplication. You may want to use others:

    Take 3 slices of a pie and ask her to describe what she sees using fractions. She will probably say, three-eighths. You can say, “I see one-eighth THREE times and then write it as 1/8 x 3. Continue with several more until she can rewrite all the fractions up to 8/8 using multiplication. Change the fractions to sixths (you better have a lot pof pizza models!) and have her do ALL of the fractions from one-sixth up to six-sixths by herself. To assess, you should mix formats, some giving her the fraction, others giving her the multiplication statement before moving on.

    3. Ok, now how do we get to 3/8 x 8 from here. I liked your explanation of cutting up ONE bar, but I’m not sure that got at 3/8 x 8. I think it was more of the meaning of 3/8 as 3/8 x 1. So let’s try the above approach using EIGHT PIES:
    “Ok, you showed me what three-eighths of one pie looks like. Can you show me another three-eighths using a second pie. Great, can you put these together for me. How many slices (eighths) altogether? Six-eighths, good! Does it make ONE WHOLE PIE yet? Ok, now take three-eighths of this third whole pie. So, how many slices (eighths) altogether? Nine slices or nine-eighths, right! Is that the same as one whole pie? Good, you remembered about improper fractions. Now do this EIGHT times with these EIGHT whole pies. How many slices (eighths) altogether?
    Yes, twenty-four slices or twnty-four eighths. How many whole pies can you make? Show me! THREE WHOLE PIES!
    This is a bit convoluted so i know you will adapt it to make sense for your daughter but the hard part is developing these ideas in a careful structured incremental way, consistently combining the visual with the symbolic. I’m guessing that Engelmann does this with his DI materials, but each child is different. You daughter may bridge the gap very quickly and say, “Alright mommy, I got it. Let’s do something else!”
    Let me know if any of this is helpful. I might post this on my blog and have readers comment on whether this is a DI lesson or whatever!
    Dave Marain

    Reply

  6. Thinking out loud here…. could we use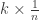 k \times \frac{1}{n} instead of 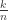\frac{k}{n} as our starting point? A heavy emphasis on unit fractions early on might help quite a bit with addition of fractions, or anything involving common denominators, later.

    The idea is choppy, but I think it deserves some thought…

    Jonathan

    Reply

  7. I think my mistake was in drawing an extra 1/8 block instead of drawing another 8 bar and then cutting it into eighths. I should have given her a source of new fraction pieces that she could have cut up mentally. But I didn’t realize until later that her “too much” complaint meant that she didn’t have enough pieces in her mind, because my mind had leaped ahead to the idea that there are an infinite number of pieces available.

    Thanks, Dave, for helping me see the abstract leap I had made. But there is no way I would do this with pizzas!

    jd2718, you are exactly right as to how the book is teaching these fractions:

    \frac{3}{8} of 8 = 3 \times \left(\frac{1}{8} of 8 \right)

    She is supposed to figure out what one fractional piece is first and then count up however many of that piece she needs, which is why I suspect the first question on this page was a typo. In every other instance, both before and after this worksheet, the book has prompted the student with a 1/x question at the beginning.

    She had already done several worksheets with that sort of problem. She also had some worksheets with fractions greater than one, but she didn’t recognize them as improper fractions. Up until this page, there were pictures of the pieces, so she just circled how many made a whole thing and wrote the answer as a mixed number.

    Moti, I think your books would be too much for her just yet—but perhaps I am selling her short. She does like a challenge, so we may try them sometime soon. In this case, however, the Miquon book was expecting her to be counting the fractions out on the blocks. The mental leap would not have been so abstract: First she would define 1/8 of 8 as a white block, then count up as many white blocks as she needed for the question at hand. But she is independent and stubborn, and she likes to work without the blocks even on problems where they would have helped her.

    Reply

  8. Denise,

    At her age, it may be too much for her to read and understand it all by herself – true. But, it would be easier for her than Miquon. The reason being that she would have the explanations of what things are and not expected to guess them. Additionally, the book is very gradual. Of course you can do blocks and such in addition, but it seems she would have preferred it without anyway.

    I think many teachers sell students short on what they can learn if guided well. Miquon didn’t guide her, so she got stuck. While I wouldn’t call it a trauma really, it’s still not useful or constructive.

    Moti
    http://www.LearningByYourself.com

    Reply

  9. Hmm. The actual definition of “improper fraction” is one in which the numerator is greater than OR EQUAL TO the denominator” [my emphasis]. Yet your daughter had no problem with 8/8 once she got past the first hurdle of what 1/8 x 8 was asking.

    That makes me wonder if the issue is the terminology rather than the concepts, or vice versa. There seems to be something arbitrary in all this. In fact, a lot of arbitrariness. Why is 7/8ths “proper” while 8/7ths is not? And particularly, why is a/b proper if and only if a < b? Based on the conversation you describe, I would swear that your daughter didn't think there was anything "not right" about 8/8.

    Makes me think of unfortunate terminology like real vs. imaginary (and complex), and the misunderstood though linguistically defensible rational v. irrational numbers. Sanity has nothing to do with them, though understanding either deeply might cost some people, including teachers, some modicum of theirs.

    One thing I try hard to avoid in my own teaching and warn teachers about doing is telling kids things that are simply not true in general (with the limit of generality being "the math typical kids are likely to actually have to or want to learn in their lifetimes" (that was somewhat ad hoc and might need work, but will have to do for right this second). So I don't recommend telling primary grade kids that "You can't take a bigger number away from a smaller number"; after all, the integers aren't all that far off in the future for them, and they may already be aware of negative numbers on some limited basis.

    So do I advocate instead launching into a deep (or even shallow) explanation or exploration of integers when kids are still working on the arithmetic of whole numbers? Of course not. It's just a matter of not making false generalizations about arithmetic that go beyond the numbers kids are working with. We can certainly say that while we don't work with the kinds of numbers that answer the question, "What is 6 – 9?" in [Grade X] or [yet], we/you will learn about them at some point." For some kids, that's a huge invitation to do a little thinking/exploring/reading on their own. For others, it simply avoids planting some absolute claim in their heads that in fact will soon become obviously false in general. Nothing to "unlearn" if you don't tell lies.

    Similarly, stating absolutely that addition, multiplication and/or exponentiation "make things bigger" or words to that effect really misleads students, who should already be asked to think about important numbers like 1 & 0 and their role in the different arithmetic operations. And thus, when they hit 3 x 1/2 the like, it should not come as a complete shock that the product is smaller than either factor.

    In sum, the less b.s. you teach kids, the less b.s. you have to unclog from their minds sooner or later. At worst, you simply have to remember to restrict just how general a given generalization is and remind students that there are lots of different kinds of numbers that they will learn about and use, so they should be careful about overgeneralizing. Better to say, "sqr(-1) is undefined for the real numbers ("real" rearing its ugly head unavoidably and misleadingly, of course), than to say, "You can't take the square root (or even root) of a negative number," because of course you certainly can, often to marvelous effect.

    Reply

  11. One representation I’ve been super excited about lately is fraction blocks that fit on the number line. Some of Gail Burrell’s recent NCTM (& other conference) talks have centered on that representation (on the TI-Nspire) and I’ve been exploring it with plain-old manipulatives here: http://mathforum.org/blogs/max/games-with-fraction-strips-and-fraction-cards/

    The point is to think of the whole unit that’s being chopped into fractions as being one of many 1-unit distances on the number line. As Christopher Danielson would say, we’re dealing with composed and decomposed units at the same time. That way you can see that 9/8 (of one) is 1/8 past one, 16/8 is 8/8 past one, etc.

    Now these are multiplication problems, so 9/8 of 8 requires shifting the unit or thinking of 8 as the whole. I really want to build a stretchy number line manipulative for multiplication, but I haven’t quite figured out how that will work yet…

    Reply

  12. Your fractions strips would work similarly to the Cuisenaire rods that Miquon assumes a child will use. When one rod is designated as the “whole”–in this case, the 8 rod–then the other rods become fractions of that whole. In particular, the white unit rod will always be 1/n of whatever n we choose as the whole.

    A stretchy number line would be a cool way of showing that transformation. We could write on elastic with fabric markers, but we’d need some way to clamp it in position after we stretched it, so the kids could line blocks and other things against it and see what they measure in the new scale. Hmm….

    Reply

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.