Fraction notation and operations may be the most abstract math monsters our students meet until they get to algebra. Before we can explain those frustrating fractions, we teachers need to go back to the basics for ourselves. First, let’s get rid of two common misconceptions:
- A fraction is not two numbers.
Every fraction is a single number. A fraction can be added to other numbers (or subtracted, multiplied, etc.), and it has to obey the Distributive Law and all the other standard rules for numbers. It takes two digits (plus a bar) to write a fraction, just as it takes two digits to write the number 18 — but, like 18, the fraction is a single number that names a certain amount of whatever we are counting or measuring.
- A fraction is not something to do.
A fraction is a number, not a recipe for action. The fraction 3/4 does not mean, “Cut your pizza into 4 pieces, and then keep 3 of them.” The fraction 3/4 simply names a certain amount of stuff, more than a half but not as much as a whole thing. When our students are learning fractions, we do cut up models to help them understand, but the fractions themselves are simply numbers.
Learn to Read a Fraction
A fraction is a number that relates to whatever is defined as one whole thing. Before a fraction can have any meaning, something has to be defined as “one whole unit.” Of course, this is true of all numbers, not just fractions. Before three can have any meaning at all, one has to be defined. Are we talking about 3 miles or 3 bags of rice or 3 spaces on the number line? Natural numbers are defined in terms of whatever one is, so fractions are no different from other numbers in this respect.
At the beginning, students need to make extensive use of fraction models. Let’s not limit ourselves to the round food model, but it is a great place to start. For the rest of this post, you may imagine “one whole unit” to be a single pizza, cut up into fractional pieces.
The first confusing thing about fractions is vocabulary: those awful words numerator and denominator. To keep them straight, our students must learn how to read a fraction. Teach your children to read fractions from top to bottom, like the pages in a book:
- The top number of a fraction is its first name, which tells how many pieces you have.
- The line in a fraction
meanscan be thought of as “divided by”, so 3/4 = 3 ÷ 4 and 5 ÷ 2 = 5/2. - And the bottom number is the fraction’s last name or family name. It tells what size the pieces are.
Now, let’s go through that a little slower…
Numerator: The Fraction’s First Name
The top number in a fraction is its first name — that is, the first thing you hear about the fraction. A fraction’s first name counts the number of pieces: 2/5 has two pieces, and 3/5 has three of them.
This makes it easy to count up the total number of pieces in a bunch of fractions:
And if you add another fifth, that would make 8/5. Add a few more to get 11/5, then maybe take some away:
counting down this time.
You can keep counting up and down forever, as long as you are only talking about fifths.
Mnemonic: It may help your students to think “number-ator.” The numerator counts the number of pieces we have.
Denominator: The Fraction’s Family Name
[Yes, this is out of order. We want our students to meet and get to know the fractions, so for beginners we focus on the names. Learning about the fraction bar comes later.]
The bottom number of a fraction is its last name, or family name. All fractions with the same last name are in the same family. The family name tells what size the pieces are — which is the same as saying how many of the pieces make one whole thing. (Remember that fractions are always defined in relationship to some whole thing.) With fourths, it takes four of them to make a whole. With sevenths, it takes seven of them to make a whole thing.
This is why, as the last name gets bigger, the fraction itself gets smaller. The more pieces your whole thing has been cut into, the smaller each piece will be.
…because both have two pieces, but 7ths are smaller pieces than 4ths.
A man is like a fraction whose numerator is what he is and whose denominator is what he thinks of himself. The larger the denominator, the smaller the fraction.
— Tolstoy
Mnemonic: It may help your students to think “down-nominator.” The denominator is the number down in the bottom of a fraction.
Put Them Together, and What Do You Get?
So what number is the fraction? It is the number that names the amount of stuff in all those pieces.
- The fraction 3/4 names the amount of pizza in 3 pieces, when each piece is 1/4 the size of one whole pizza.
- The fraction 13/5 names the amount of pizza in 13 pieces, when each piece is 1/5 the size of one whole pizza.
- The fraction 8/8 names the amount of pizza in 8 pieces, when each piece is 1/8 the size of one whole pizza.
But it is important to remember that the fraction itself is NOT the same as those pieces of pizza. If I had 3/4 of a pizza, it would be the same amount of stuff even if it had not been cut up — for instance, if my daughter came through and cut out as much of the pizza as she wanted, without bothering to cut the rest apart. And the whole pizza is 8/8 of a pizza, even before the first cut is made.
As we work our way toward a solid understanding of fraction operations, we will often come back to our fraction models to ask these questions:
- What size are the pieces?
- How many of them do we have?
The Line in a Fraction Can Be Read “Divided By”
Every fraction is also a division problem — or rather, it is the answer to a division problem. For instance, the fraction 7/3 names the amount of pizza each person would get, if we divided 7 pizzas evenly among 3 teenage boys:
Think of the division symbol “÷” as a miniature picture of a fraction. The dots stand for the numerator and denominator.
This is why the remainder in a division problem turns into a fraction. Consider those 3 teenage boys fighting over the 7 pizzas. It is easy to give them each 2 whole pizzas, but what shall we do with the remaining one? We have to cut it up, and each boy will get 1 ÷ 3 of it.
Whatever our remainder is, that becomes the numerator of our remainder-fraction. The denominator is whatever we were dividing by.
Knowing that the line in a fraction means “divided by” will be important in solving complex fractions like this MathCounts puzzler:
…or when our students meet algebra monster fractions like:
So we will keep reminding our students of this fact throughout middle school or junior high:
A fraction
iscan be written as a division problem.


Nicely said.
Article on fractions revealed overcomed certain misconcepts. The students have many misconception about fractions. After reading your article , I am able to deliver the concept very easily to my students. Thanks for giving such a good article.
Hi my name isChris and I love your book in maths
Thank you, Chris. 🙂
The form of a/b does not automatically mean it is a fraction. So we must not teach children to say just because it is 2/3 so it is a fraction.
It is also debatable to say that 2/3 is just an one number. just like 23 can be expanded as 2 numbers as well. The form 2/3 is simply an invented notion to express part out of whole and that is it. This form is an most effective way of expressing part out of whole concept.
2/3 can be expressed as picking 2 out of 3 and this is another form of “fraction”, it is equivalent to say “cut equally 3 parts and 2 parts are chosen” in pure number sense but in real life experience the meaning might be different. so the form of a/b without any explanation at all, we are just not sure what it really means, it can be a fraction, can be a pure number, can be 2 chose out of 3 and can be 2 out of whole piece being cut, and can be a 2 compared to 3 as a ratio.
The article is confusing if it does not explain the form of a/b from a broad sense but instead try to narrowly define a/b as simply a fraction.
i totally agree with you , Frank Ho . Denise has a huge misconception about fractions , and totally reads fractions in a wrong way . Please read my opinions here , https://www.math.mobi/2018/12/how-to-read-fractions.html
The next article in this series will discuss the various models we use to understand fractions, such as pieces of a whole thing (the model used in this article) or parts of a group (such as picking 2 out of 3).
For a discussion about expanding fractions into more than one number (like 23=20+3), keep your eyes open for the Alexandria Jones series on Egyptian fractions, coming in January 2008.
Nice explanation Denise! You must get a lot of students thinking about slices to repeatedly reinforce things ” …would be the same amount of stuff even if it had not been cut up…” What is the common mistake that your students make here? Do they just always think one out of two pieces is 1/2 even if the piece is only a quarter pizza?
Frank: Not sure why the big focus on what a/b means. Doesn’t it always mean a fraction? I’ve never heard it referred to as “parts of the whole” except as an explanation, which to me is just a long way of saying “fraction” or “division” anyway. a/b evaluates to a number all the time if a and b are numbers, doesn’t it?
I think it is instructive to teach a/b as a way of writing a single number, especially if you pair it eventually with numbers that cannot be written in decimal. eg, 0.333…. can be written exactly as 1/3. Not sure at which grade that occurs.
One problem my young students have is understanding how a fraction can be bigger than a whole unit. How can there be such a thing as 8/5, when you only have 5 pieces to begin with? (I wrote a blog post awhile back about my youngest daughter’s traumatic encounter with just such a concept.)
When I look at the confusing questions in that frustrating fractions quiz, I think most of them have to do with not understanding that a fraction is a single name for a certain amount of stuff, and thus it has to be treated as one (admittedly rather weird) number. Students who think of a fraction as two numbers will see no problem with a jumbled, mis-remembered rule like, “To add two fractions, I add the top numbers and add the bottom numbers.”
Also, by defining fractions as a certain amount of stuff, I hope to broaden my readers’ vision to see beyond the round food model. Many in my audience are homeschooling parents with no training in math other than what they studied in school years ago. If the teachers in Liping Ma’s study were so limited in their understanding of fractions, how much more limited are those of us who studied under such teachers.
I think it’s also useful to think of a fraction as either “a division problem” or “the answer to a division problem”. Thinking of a fraction as a certain representation of a given number or “amount of stuff” is useful too.
Nice
Also take a look at http://englishresort.blogspot.com/2008/12/how-to-read-fraction.html
how to read 3/4 three fourths or three quarters, what about 6/7 – six sevenths or six over seven ? tx
Cicik, any of those readings will work, although I think “three fourths” and “six sevenths” communicate the meaning best. They are parallel to measurements like “three inches” or “six grams.” The “this over that” reading becomes more common in algebra, where you will find yourself working with very complex fractions.
what??? Im 22 and dont even understand fractions…im so confused and trying to surff the internet to see if i can figure it out but nothing…
okay, i dont know but heres the problem 7/12 ( , =) 2/3…i wrote the pizza circle out and 7/12 is greater…right? also i put it in the computer but it showing me wrong….?
Your explanation on fractions is really helpful for me to teach a struggling math student! 🙂 He understands it much faster when I used your method. Thank you!
What is the relationship between fractions of the same family. Using three family
proper fraction, improper fraction and mix fraction
Morlon, I am not sure quite what your questions means. Fractions of the same family (as I am using the term) means fractions with the same size pieces. In proper mathematical language, these are fractions with the same denominator — that is, the same bottom number.
For the other words you mentioned: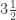 .
.
proper fraction = a fraction in which the numerator (top number) is smaller than the denominator
improper fraction = a fraction in which the numerator is not smaller than the denominator
mix fraction = I’m not sure, but it’s probably what I would call a “mixed number”, which means you write a whole number and a fraction together as an implied sum, like
Thank you for using the proper names. Did you put a glossary in your new book?
Those technical words are very helpful for fractions.🙂
I don’t have a glossary in my book, but there are several math dictionaries and websites online. Maths Is Fun is a great source:
https://www.mathsisfun.com/definitions/
Or check out the Math Dictionary for Kids:
http://www.amathsdictionaryforkids.com/
i thank you for teaching mii more about fractions
In the beginning of this post you say, “A fraction is not something to do”, but at the end of the post you say, “A fraction is a division problem”. Isn’t that contradictory?
You’re right, Jackie, that sounds like a contradiction. Perhaps I should have said it this way: “A fraction can be written as a division problem.”
What a great explanation of fractions. Sometimes it helps to hear things in a different way to help you become a better teacher, thank you for that. I loved the quote from Tolstoy! I did find the section on “Put them together and what you get” to be a little confusing…maybe there is another way to explain that…what about a visual!
Please help me I know that 3/4 of 8 balls is 6 by 3*8 will give you 24/4 will give ,6 but how will I explain it practically?
One of the best ways to think through a fraction puzzle is what Ed Zaccaro calls “Think 1.” Can you think of what 1/4 of your set would be? Then use that to figure out how much would be three of those fourths.
Learning how to read a fraction and knowing how to do the basic mathematical operation on it is a lesson that we should never miss and a must to learn.. It is a foundation that should be instilled on the minds of a young students. But sometimes doing it manually may result in a wrong answer. That is why I used a tool to confirm that the computation is correct. For checking if the calculation of fractions is correct, I used an app which shows the correct answer and display the step by step solution. It is actually a fraction calculator from http://www.fractioncalc.com. It is very useful in solving fraction and a very good tool to be used both by teacher and student for reference if their answer is correct and if their solution is right.