Pondering Large Numbers

[Feature photo above by Paolo Camera (CC BY 2.0) via Flickr.]

Half of our students were missing from this month’s homeschool teen math circle, but I challenged the three who did show up to wrap their brains around some large numbers. Human intuition serves us well for the numbers we normally deal with from day to day, but it has a hard time with numbers outside our experience. We did a simple yet fascinating activity.

First, draw a line across a page of your notebook. Label one end of the line $20 (the amount of money I had in my purse), and mark the other end as $1 trillion (rough estimate of the US government’s yearly overspending, the annual deficit):

• Where on that line do you think $1 million would be?

Go ahead, try it! The activity has a much greater impact when you really do it, rather than just reading. Don’t try to over-think this, just mark wherever it feels right to you.

The kids were NOT eager to commit themselves, but I waited in silence until everyone made a mark.

• Okay, now, where do you think $1 billion would be?

This was a bit easier. Once they had committed to a place for a million, they went about that much farther down the line to mark a billion.

How Much Is a Million?

Twenty dollars is a normal, rather small amount of money. A million dollars is huge, the kind of money my students can only dream about, and a billion dollars is unimaginable. Their gut instinct rebels at putting these marks very close to the purse-money end of the line.

On the other hand, it’s natural for the kids to suspect a trick. Why would the teacher insist that they make a mark, unless she’s trying to trap them?

The first girl made her mark in the middle of the line, but the more she thought about the possibility of a trick, the more it bothered her. She erased the mark and made a new one about 1/3 of the way between the purse and the trillion.

The boy marked much closer to the purse, about one-tenth of the way along the line.

When he saw that his neighbor’s mark was even closer to the purse, he declared, “She’s probably right!”

How Much Is a Billion?

Once the initial commitment of a guess has been made, the students didn’t struggle as much with the second mark. Each of the girls approximately doubled the distance of their first mark from the $20 end of the line. The boy erased the label on his first mark and renamed it a billion, then cut that distance in half and called the new mark a million.

It’s interesting the way our brains work for this sort of question — it’s is actually more logarithmic than linear. The students’ responses are typical of how many adults visualize large numbers:

• a thousand is roughly twice as much as a hundred
• a million is roughly twice a thousand
• a billion is roughly twice a million, etc.

No, the above statements are not true, but they represent what the numbers feel like to many people. We can easily visualize the small numbers that we commonly work with, but we must rely on vague notions of “big, bigger, biggest” to deal with large numbers. Our intuitive number sense seems to work like a semi-logarithmic scale, with the small numbers evenly spaced and the bigger numbers crowded together at the end.

Linear Number Line for Small Numbers

Logarithmic Number Line for Large Numbers

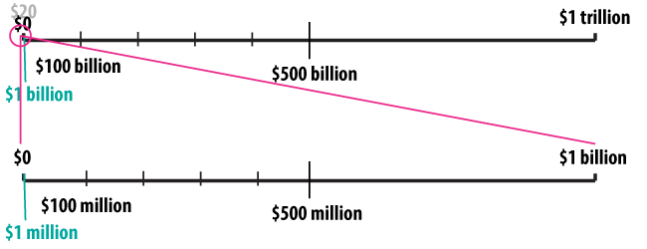
So How Much Is It, Really?

Going back to our original line, we can see that the $20 in my purse is so small compared to $1 trillion that we can count it as zero. A trillion is a thousand billion, so half of that would be $500 billion. Mark that on your line:

Split that into five chunks to find $100 billion.

Now imagine dividing the first chunk into 100 small pieces. One of those pieces would be $1 billion:

And how much is a million? We can’t see it on this scale, but imagine magnifying the tiny chunk between 0 and 1 billion out to the size of the original line. Then a billion is a thousand million, so half of that would be $500 million. Split that into five chunks to find $100 million. And imagine dividing the first chunk into 100 small pieces:

More Fun with Large Numbers

If your students want more experience with mind-blowing large numbers, we also did page 23 of this file, the section called Large Numbers and Everyday Things:

• The Infinite
  From the Discovering the Art of Mathematics (DAoM) library

Small Numbers Are Equally Hard

As Mike Lawler and sons discover in this video, very tiny numbers are just as difficult to imagine as very large ones:

Can You Count to a Trillion?

Our human difficulty in visualizing large numbers explains why politicians feel comfortable throwing around huge budget amounts, confident that their constituents won’t understand how horrifying the numbers really are.