Math Teachers at Play #70

Posted on by Denise Gaskins

800px-Brauchtum_gesteck_70_1[Feature photo above by David Reimann via Bridges 2013 Gallery. Number 70 (right) from Wikimedia Commons (CC-BY-SA-3.0-2.5-2.0-1.0).]

Do you enjoy math? I hope so! If not, browsing this post just may change your mind.

Welcome to the 70th edition of the Math Teachers At Play math education blog carnival — a smorgasbord of 42+ links to bloggers all around the internet who have great ideas for learning, teaching, and playing around with math from preschool to pre-college. Let the mathematical fun begin!

By tradition, we start the carnival with a puzzle in honor of our 70th edition. But if you would like to jump straight to our featured blog posts, click here to see the Table of Contents.

PUZZLE: 70 IS WEIRD!

This puzzle involves factoring, which means breaking apart a number by multiplication. To factor a number is to find two numbers that can multiply to make the number you started with.

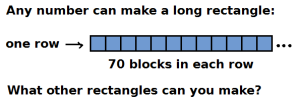
1x70rectangle

The easiest way for young students to understand factoring is by making rectangles: the sides of each rectangle (the number or rows, and the number of blocks per row) are the factors of the original number. Get 70 small blocks, pennies, or dried beans. Can you arrange them into same-length rows to make a rectangle?

Like every number, 70 can make a long, one-row rectangle (with 70 blocks per row). This shows that 1 \times 70 = 70 , which means that 1 and 70 are both factors (or divisors) of 70. But only 1 is called a “proper divisor” of 70, because in math a proper divisor must be smaller than the original number.

  • How many proper divisors of 70 can you find?

If the proper divisors of a number add up to exactly that number (like 1+2+3=6), then we call it a perfect number. If they add up to more than the number you started with, it is an abundant number. And if the proper divisors add up to less than the original number, we call that number deficient.

  • Which kind of number is 70?
  • What other abundant numbers can you find?

For most abundant numbers, you can add some of their proper divisors to make the number. For instance, there are several ways to add some of the factors of 12 together to make a total of 12. But no matter how you add the factors of 70 together, you can’t get exactly 70. Try it and see! Mathematicians call abundant numbers like 70 weird numbers.

  • Can you find one other weird number that is less than 100?

[Was this puzzle too elementary for your kids? Jump ahead to the Bonus Puzzle for Older Students.]

Table of Contents

And now, on to the main attraction: 42 blog posts of mathy awesomeness. Many of the articles were submitted by their authors; others were drawn from the immense backlog in my rss reader. If you’d like to skip directly to your area of interest, try these links:

EARLY LEARNING ACTIVITIES

Chamberland-borromean_5

“I have long been enchanted by the aesthetic side of mathematics. Most people view mathematics as a collection of tools and procedures and get mired in the mechanics. Mathematical art communicates the essential beauty found in mathematics.”

— Marc Chamberland
Borromean Five

  • Christopher and Tabitha “have been playing with the multiplication machine off and on for a few months now. We have never once used it for learning multiplication facts, but we have had a ton of math-learning fun with it.” Tabitha describes her analysis of Patterns on the multiplication machine, and her dad explains how to start math conversations with your own kids.
  • Patrick teaches a New Year’s Eve gathering of neighborhood tots to play Low-Sham-Bow (a mathy modification of Rock-Paper-Scissors) and discovers that he is Not Good at Math Games.
  • Mashka introduces her preschool/kindergarten math circle to thinking about systems in Tricky PreK Math, Lesson 8 – Year 2. Then she challenges the students to a working-together puzzle game. “We only had a couple of minutes to play, but it came out very funny with everybody tangled. Almost all of them were cheating (their eyes were open) and they still couldn’t make a square (or even get untangled).”
  • Claire’s daughter continues to enjoy Mr Men School: Little Miss Naughty, with lessons including days of the week, matching, measurement, and even a little bit of workbook math. “This week was about her familiarizing herself with all the tools inside the box. I didn’t set her much specific work, instead let her play with the box whenever she asked.”
  • Check out this mom’s creative solution for dealing with Distractions and delays in completing a math workbook page. “She wanted to stop and draw a hat on the duck, only cross them out a certain way, or draw other designs that flowed out from her imagination. Meanwhile, she was taking FOREVER to go over her math…”

[Back to top.]
[Back to Table of Contents.]

ELEMENTARY EXPLORATION AND MIDDLE SCHOOL MASTERY

Jespersen-magic_sphere_with_lizards_0

“Magic woodcarving is the art of carving a piece of wood into parts that are loose, but cannot be separated… The “magic” becomes apparent when you manipulate the object and discover that its parts are in fact loose and able to move slightly among each other — a very surprising experience…the lizards are cut loose and are able to move slightly when you manipulate the ball.”

— Bjarne Jespersen
Magic Sphere with Escher’s Lizards

  • Maya links to the free (CC-licensed) Happy Maths Series from Pratham Books: “These are mathematics books with a difference. There are more stories here than problems! So read the stories, absorb the mix of facts and fiction and enjoy teasing your brain.”
  • Julie rounds out a unit study on Ancient Rome by creating a free printable game: Roman Numeral Bingo.
  • Hwee offers an arithmetic challenge: “Now that we are very familiar with straightforward addition, let’s try our hand at finding the sum of all the numbers in a range, say from 26 to 765, without using a spreadsheet or calculator…” Find out how her son Tiger works his way through to success in When Everything Adds Up.

[Back to top.]
[Back to Table of Contents.]

ADVENTURES IN BASIC ALGEBRA & GEOMETRY

Kaplan-square_weave

“Most Islamic star patterns can be rendered in an interlaced style, wherein the pattern is decomposed into distinct strands, and each strand weaves alternately over and under the strands it crosses… The physical act of weaving these works can help reinforce one’s intuition for the mathematical structure of the underlying designs.”

— Craig Kaplan
Woven Islamic Star Pattern 1

  • “Algebra. Sounds like a really sophisticated maths idea, doesn’t it?” ask Hwee. “The truth is, most children already intuitively know the basics of algebra without calling it that.” Read about her 4th-grade son’s introduction to algebra in Finding the Balance.
  • “If you’ve read the recent article My Daughter’s Homework is Killing Me, then you know that parents all over our country are scratching their heads, wondering when homework got so dang hard.” But Jennifer offers a tasty solution in 5th Grade Algebra and Candy.
  • A good math problem can stick with you for years. Ben describes how a pattern that he played with in 5th grade and rediscovered in algebra has recently come back to enlighten him anew: Undiscovered Math. “I suffered ten seconds of stunned disappointment that my treasured conjecture was nothing but old hat. Then I smiled. When you’re standing on a mountain, you don’t care that others have stood on that same spot before. You’re just enjoying the view.”
  • Mr. Gregg’s class experimented with Tessellations and created some beautiful patterns. Can you identify the types of symmetry in each pattern?
  • There’s a problem with math problems, according to Geoff: “Not all problems are created equally and some may be more easily acquired and delved-into by students.” But he shares several accessible and enjoyable math problems in his Problem Based Learning Starter Kit.
  • Have you seen Fawn’s new Math Talks blog? Follow her students as they think about mental arithmetic, visual algebra and geometry patterns, and more. Start here: How we do math talks.

[Back to top.]
[Back to Table of Contents.]

BONUS PUZZLE FOR OLDER STUDENTS

The ancient Pythagoreans thought that all things in the universe could be described in ratios (simple fractions made of whole numbers, like 3/4). And they knew that length of the diagonal in a unit square had to be the square root of 2. But they had trouble finding a ratio that, when you square it, would exactly equal 2:

\left ( \frac{1}{1} \right )^{2} = 1

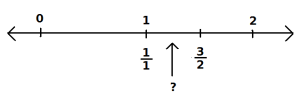
70 is a Pell number

That’s too low. We can do better:

\left ( \frac{3}{2} \right )^{2} = \frac{9}{4} = 2\frac{1}{4}

Now it’s too high. Can we get even closer?

\left ( \frac{7}{5} \right )^{2} = \frac{49}{25} = 1 \frac{24}{25}

And now our number is too low again, but we are definitely closing in on the goal. If we keep trying bigger numbers, we can surely narrow the gap.

  • Can you find the next fraction?

The next fraction will make a square that’s too high, but that is even nearer to 2. You will need to go up to double-digit numbers. Make fractions with numbers between 10 and 20, and see how close you can get to the square root of 2. Test your fractions by squaring them. No calculator: Pythagoras didn’t have electronics!

  • Do you see a pattern for these fractions?

The denominators of the fractions that come closest to the square root of 2 are called Pell numbers, and 70 is one of them. Like the Fibonacci series, each Pell number is related to the numbers that come before it.

  • Did you figure out the pattern? Fill in the Pell numbers:
    1, 2, 5, ___, ___, 70, ___, ___, …
  • Find the numerator that goes with denominator 70 to make a fraction that is almost equal to the square root of 2.

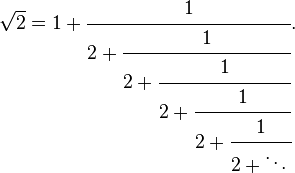
root2fraction

To check your answers to the Pell number puzzle, use this continued fraction. Each stage of the fraction (up to one of the plus signs, and ignoring everything after it) simplifies to a corresponding Pell fraction.

Read more about the Pythagorean problem with the square root of 2 here:

[Back to top.]
[Back to Table of Contents.]

ADVANCED MATHEMATICAL ENDEAVORS

Fathauer-curve

“I’m fascinated by beautiful and complex forms both in mathematics and in the natural world. Combining mathematics with artistic creativity allows me to explore and express these ideas in unique images and forms.”

— Robert Fathauer
Iterated Curve

  • Chris makes a New Year’s Resolution to keep his students puzzling their way through the months. You can do it, too, with these January 2014 Problem Calendars!
  • You’ve probably heard that math can be beautiful. (And surely the art illustrating this carnival post proves that is true!) Dan reviews the book Beautiful Geometry, “a rare opportunity to listen in on an extended and fascinating dialog between Math and Art,” in Art for math’s sake.
  • “Imagine Ug, the first ever mathematician. She’s at her cave, rocking her baby (on a rock, of course) and thinking about numbers…” Dr. Mike spins a story about the repeated discovery that something is missing, in answer to the question Are Complex Numbers Real?
  • Sue gives herself the challenge of Explaining Calculus using the Up-Goer Five Text Editor, which allows only the 1,000 most common words. “Here are some of the words you can’t use: math, slope, steepness, circle, curve, and infinity.” Tough! Check out her description, and then try it for yourself. Can you do better?
  • “After reading my end-of-semester surveys,” says Shireen, “too many students were mixing up what to do when and why when finding the maximums and minimums of functions.” So she comes to the rescue with a three-part Calculus Graphical Organizer.

[Back to top.]
[Back to Table of Contents.]

PUZZLING RECREATIONS

DeComite-circles

“Sets of tangent circles can be generated in several ways : Apollonian gaskets, Steiner’s chain, Doyle Spirals… Once you have such a set of tangent circles, you can apply geometric transformations preserving those tangencies : circle inversions, Mobius transform. Combining all those tools let you create an infinity of arrangements.”

— Francesco De Comité
A Whiter Shade of Deep Purple

  • Ben poses a series of Tic-Tac-Toe Puzzles and elaborates on the difference between a puzzle and a game. “As a math teacher, I mostly traffic in puzzles. I try to engage my students with tricky ideas. I encourage them to work out the possibilities, to master the scenarios, to boil their understanding down to steps that can later be applied automatically. But when it comes to math itself, I hope my students see it as more than a collection of puzzles. I hope they see it as a game, full of promise and possibility. I hope math never exhausts its ability to surprise, to stump, and to delight them.”
  • Rodi’s math circle tackles several challenging problems in Pirates, Prisoners, and Psychopaths. “An hour-long mathematical struggle ensued. Actually, the struggle was much more than mathematical. Some of the students were troubled by the pirates’ rules of distribution. There was a desire for more ethical rules among some students, and a countervailing attitude among others of c’mon dudes, they’re pirates!”
  • My entry to the carnival this month is a math puzzle extravaganza for all ages. Spend quality time with your family, strengthening mental muscles with the 2014 Mathematics Game.

[Back to top.]
[Back to Table of Contents.]

TEACHING TIPS

screened_icosahedron-1800x1200

“Since a very early age, I have had a powerful and inescapable fascination with order, symmetry, and pattern. For these reasons, my artistic pursuits have always centered around the innate beauty found in mathematics, especially tesselations, polyhedra, and fractals.”

— Phil Webster
Screened Icosahedron

  • What can you do with an “awesome class of students who were lacking in number sense [and] who were very used to being unsuccessful in math”? If you’re Sadie, you start a Counting Circle: “I am unable to live with myself if I allow students to graduate high school (pass my class) without having mental math strategies. It is equivalent to allowing a student to graduate from high school without being able to read. I refuse to be part of this movement anymore.”
  • Did you know that teaching children to quickly estimate numbers without counting may improve their ability to do regular arithmetic? Maria tells how in Math mind hacks: Guesstimate. Be sure to check out the rest of the tips in her Math mind hacks series, research-based snippets you can immediately use to “hack” your brain for math productivity and well-being.
  • “In the beginning, there was a calculus teacher complaining about students’ lack of a good definition for slope…” and by the end, Tina had written a book that spans math from elementary to high school. Now she offers us Nix the Tricks: The Book as a free download. Read it and share!
  • Crystal says, “I try to help my daughters solve problems that are just a little out of their reach using information they do know.” Check out her introduction to Socratic questioning in Good Question.
  • Maria demonstrates how to convert textbook exercises From CLOSED math problems (with one answer) to OPEN ones. “I don’t mean you’d need to do this to every problem in the book,” she explains, “but do it to SOME so that your children/students can have the opportunity of seeing that math can be ADVENTUROUS — you can be CURIOUS in math class — and it can even be FUN! It’s not just about spitting out correct answers to calculation problems.”
  • Can you create a math-related “lesson” on the fly that will leave a smile on a stranger’s face? Gerry describes some of the games and puzzles he has used in teaching and cites several sources for additional inspiration. Read this excerpt from his new book Letters to a Young Math Teacher on the IMACS blog.
  • “It wasn’t until three years into homeschooling my kids that I began to get a glimpse of what maths really is,” Lucinda says. “I’m still at the start of this journey of discovery so I’m certainly no expert, but I’d love to share with you some of what I’ve learned so far.” Check out her extensive list of resources in How to Help Your Child Fall in Love with Maths (Even if They Hate It).
  • “So many people love the idea of unschooling and are even tempted to give it a go, but often there is one huge stumbling block… maths. Very few parents seem to be confident that their children will learn all the maths they need to know, without being prodded along by some kind of intentional instruction.” Sue shows us how to start small by strewing our children’s world with Bite-Sized Pieces of Unschool Maths.
  • Finally, if you enjoyed reading all these blog posts, you will find many more great ideas about teaching math in Geoff’s Math Blogging Retrospectus 2013, a compendium of inspiring math education posts.

[Back to top.]
[Back to Table of Contents.]

GIVING CREDIT WHERE IT’S DUE

Mehta-phi-tri-cmy

“Being an architect by profession and an artist by passion, I have been working on devising various methods and algorithms to marry mathematics and aesthetics… The basic shape is formed by combining two equilateral triangles with their sides in golden ratio. This shape is fractally tesellated into the same shape, its mirror and a trapezium.”

— Chirag Mehta
Phi-Tri-CMY

The images in this month’s carnival are my personal favorites from 2013 Bridges Conference Art Exhibit, and the quotations are from the artists.

And that rounds up this edition of the Math Teachers at Play carnival. I hope you enjoyed the ride.

The next installment of our carnival will open sometime during the week of February 10-14. If you would like to contribute, please use this handy submission form. Posts must be relevant to students or teachers of preK-12 mathematics. Old posts are welcome, as long as they haven’t been published in past editions of this carnival.

Past posts and future hosts can be found on our blog carnival information page. We need more volunteers. Classroom teachers, homeschoolers, unschoolers, or anyone who likes to play around with math (even if the only person you “teach” is yourself) — if you would like to take a turn hosting the Math Teachers at Play blog carnival, please speak up!

300_stars_in_orbit_1

“My earliest love of mathematics came when I realized its utility in creating beautiful things. As a third grader (and ever since), I spent countless afternoons drawing stars and patterned shapes with a protractor or compass.

“In my art I sometimes try to illuminate the complex structure and interconnectedness of simple, patterned objects. I’m compelled to understand complete spaces of related works and how my choices as an artist locate me within that space.”

— Paul Salomon
Stars of The Mind’s Sky

One thought on “Math Teachers at Play #70”

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.