Photo by Song_sing via flickr. In this Homeschooling Math with Profound Understanding (PUFM) Series, we are studying Elementary Mathematics for Teachers and applying its lessons to home education.
My apologies to those of you who dislike conflict. This week’s topic inevitably draws us into a simmering Internet controversy.
Thinking my way through such disputes helps me to grow as a teacher, to re-think on a deeper level concepts that I thought I understood. This is why I loved Liping Ma’s book when I first read it, and it’s why I thoroughly enjoyed Terezina Nunes and Peter Bryant’s book Children Doing Mathematics.

Multiplication of whole numbers is defined as repeated addition…
— Thomas H. Parker & Scott J. Baldridge
Elementary Mathematics for TeachersMultiplication simply is not repeated addition, and telling young pupils it is inevitably leads to problems when they subsequently learn that it is not… Adding numbers tells you how many things (or parts of things) you have when you combine collections. Multiplication is useful if you want to know the result of scaling some quantity.
— Keith Devlin
It Ain’t No Repeated Addition
Many Models of Multiplication
All of us, whether children or adults, cling to our first impression of anything until reality forces us to revise that impression — and we tend to resist such revision as long as possible. Therefore, as homeschool parent-teachers we want to make sure that our students’ first impression of a topic is worth hanging onto, that it will serve as a solid foundation for future learning.
For many of us, our first impression of multiplication was as “repeated addition.” Unfortunately, this is NOT a definition worth clinging to. I’ve written before about What’s Wrong with “Repeated Addition”? (and Multiplication Is Not Repeated Addition: Update), so I won’t repeat that argument here. But let me point out several important mathematical situations where repeated addition is definitely not multiplication:
- Triangular Numbers
- Odd Numbers Make Perfect Squares
- Infinite Series
- Harmonic Series
Can you identify what is different about each of the above situations compared to what our textbook authors Parker & Baldridge meant when they defined multiplication as repeated addition? That difference is the key to helping our children understand multiplication.
Do not limit your children to a single model of multiplication, especially a model as fragile as “repeated addition.” Instead, explore the many real-life Multiplication Models collected at the Natural Math website.
Point out to your children how almost every multiplicative situation has one significant feature: a ratio or this-per-that quantity.
- Sets
items per set
- Skip Counting
steps per skip
- Number Line Jumps
spaces per jump
- Rectangular Array
rows per column (or columns per row)
- Time and Money
dollars per payment
- Fractals
copies per iteration
- Combinations
choices per option
When we help our students learn to recognize this-per-that situations, we give them a tool that will serve them well as they deal with elementary word problems and will also prepare the way for proportional thinking in algebra and beyond.
The Mad Scientist Model of Multiplication
Multiplication is like a mad scientist’s ray gun that can enlarge or shrink things according to which scale factor the scientist sets:
[number] [number] = [scale factor] “times the size of” [original amount]

That is where we get the word times for the multiplication symbol, though I also teach my students to use the word of, especially when multiplying with fractions or percents. If the scientist sets the scale factor at 1.0, that will leave the item exactly the same size. Any number greater than one will make the item grow, while a number less than one will shrink it.
2.9 6 = 2.9 times the size of 6
5 8 = 5 of 8
12 =
of 12
55% 90 = 55% of 90
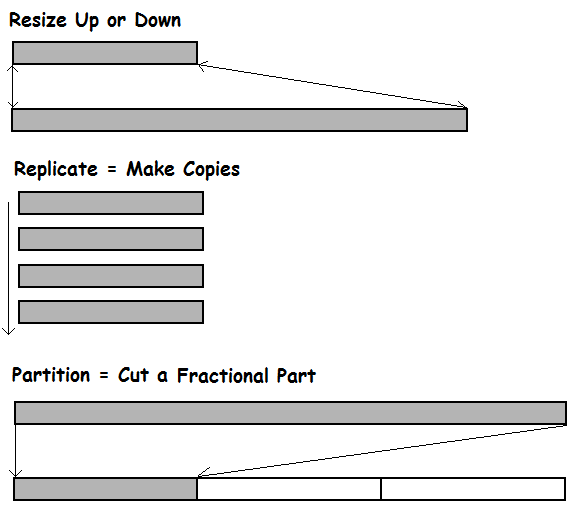
The ray gun has another setting in addition to the scale factor. This setting controls the type of growth or shrinkage. The scientist can make something grow by resizing (changing the size) or by replication (copying). With his Resize setting, he can turn a cockroach into a monster 413⅞ times its original size. Then he can switch to the Replicate setting, which creates multiple copies of the monster, until he has a whole army of giant cockroaches ready to attack.
Similarly, the mad scientist can shrink things by resizing or by partitioning (cutting it down to a fractional part).
The Resize setting may be used with any scale factor, but the Replicate setting needs a whole number scale factor (how many copies?), and the Partition setting needs a simple fraction or percent scale factor.
The mad scientist’s Replicate setting is like the common textbook description of multiplication as repeatedly adding the same amount. If the mad scientist’s wife fixes six bowls of stew and lines them up in a row, she can use the Replicate setting to create row upon row of additional bowls, until she has more than enough stew to feed all the minions. Our students can use replication to model multiplication with rows of blocks, making an original row and then copying it again and again, until they have as many rows as the scale factor says.
Teaching Multiplication with Cuisenaire Rods
- Introducing Multiplication as Rectangles with Cuisenaire Rods at Education Unboxed
The rectangular array/area model of multiplication is a powerful way of thinking that will help our children understand many mathematical topics and real-life situations.
- Multiplication/Strategy Game using Cuisenaire Rods at Education Unboxed
A suggested modification: Start the players’ rectangles from opposite edges of the graph paper, letting their “conquered” territories grow toward the center.
* * *
“PUFM 1.5 Multiplication, Part 1” is part of the Homeschooling with a Profound Understanding of Fundamental Mathematics Series. Go to the previous post. Go to the next post. Or start at the beginning.
This blog is reader-supported.
If you’d like to help fund the blog on an on-going basis, then please head to my Patreon page.
If you liked this post, and want to show your one-time appreciation, the place to do that is PayPal: paypal.me/DeniseGaskinsMath. If you go that route, please include your email address in the notes section, so I can say thank you.
Which I am going to say right now. Thank you!
“PUFM 1.5 Multiplication, Part 1” copyright © 2012 by Denise Gaskins. Image at the top of the post copyright © Song_sing via Flickr (CC BY 2.0).

But the Khan Academy *says* that multiplication is just repeated addition, so it must be so, right?
Thanks for an exploration that doesn’t just make it complicated.
Lol!
Sal is in good company — lots of people say that. It makes sense at the elementary level, when we’re just working with whole numbers, and we don’t think far enough ahead to realize that it falls apart with fractions. Or even just with zero: How can 0x5 mean to add 5 to itself zero times? It’s nonsense.
Repeated addition a good mental math thinking strategy for multiplication, as long as it’s just one part of our arsenal, but it collapses too easily to make a definition out of it.
I’m wondering how it falls apart with fractions. A fraction has a decimal values. You could add the decimal values a repeated number of times.
Also, here’s what I found in the Mathisfun dictionary:
http://www.mathsisfun.com/definitions/multiplication.html
“But as well as multiplying by whole numbers, we can also multiply by fractions, decimals and more.
For example 5 × 3½ = 5 + 5 + 5 + (half of 5) = 17.5
So, I don’t see how repeated addition breaks down with fractions.
Why do you use a definition for multiplication that is only for whole numbers? That is why it would all apart for fractions, unless you include rational numbers in the definition, not just whole numbers.
Yes, Kim, that is exactly the problem behind treating “repeated addition” as a definition for multiplication. It cannot possibly be a definition, because there are many classes of number to which it’s not possible to apply repeated addition.
Fractions, for example. Yes, you can think of 5 × 3 1/2 as meaning “Add 3 1/2 to itself 5 times” or even as “Add five to itself 3 times and then add a half of five more.” (Though the last one is circular reasoning because addition has no way of defining a “half” of five.) But there is no way to think of something like 1/5 × 1/3 with repeated addition. How can you add any amount to itself a fraction of a time? It’s nonsense.
Or consider irrational numbers. We want our students to learn that the area of a circle is π × r2. But how can you add any amount to itself an irrational number of times? Again, nonsense.
We need to give our students a more robust understanding of multiplication than the “repeated addition” mantra. Keith Devlin recommended the idea of multiplication as scaling one number by another. I’ve put my focus on ratio/proportional relationships but also attempted to use the merge several concepts into my “mad scientist’s ray gun” model above.
You do not have to accept either of those approaches. Perhaps you have a better, more generally applicable suggestion?
I really think you’re too hard on repeated addition. 0×5 is “zero fives”, which is hardly nonsense! Ask a child how much she can buy with zero nickels and she’ll probably give you the right answer. Ask her how she needs to scale or partition a nickel to buy a chocolate bar, and she might be stumped 🙂 Fractions are also fine. 0.5×10 is half a ten. 2.5×10 is two and a half tens.
Repeated addition is an easy explanation for any number problem until maybe you hit about grade 10 or 11 and get matrices, but then matrices are abstract objects anyway. In the end, multiplication is an invented and abstract concept. Nobody ever wants to multiply in real life, they want to repeatedly add, or scale, or forecast, or whatever and multiplication is the tool they use.
Young kids who DON’T realize that multiplication is a way of organizing and adding groups of objects find multiplication mysterious in my experience. To me, the early math is mainly bringing concepts back to counting, so multiplication is not even repeated addition because addition is counting. There are many algorithms and tables so if the focus is on those then a disconnect often occurs. If the child can analyze an algorithm in terms of counting then it’ll be solid learning.
Ah, but “zero fives” is not at all the same thing as saying “add five to itself zero times.” Nor is “half of a five” the same as saying “add five to itself half a time.” What you are describing is not repeated addition.
Even so, in my mind the biggest trouble with telling our children that multiplication is “just repeated addition” is that we have not given them any way to distinguish the two concepts. Children desperately need a way to identify which types of situations call for addition/subtraction as opposed to multiplication/division. Otherwise, they will never be able to work word problems — and in the world of real life, ALL problems are word problems!
Also, the difficulty appears long before matrices. Students who can’t make a conceptual distinction between addition and multiplication (because one is “just” a special version of the other) have absolutely no way to make sense of the way fractions behave. The rules for working with fractions will be abstract and meaningless, handed down from on high and accepted on the teacher’s authority. What a terrible way to learn math!
Mmm, I see what you’re saying (maybe :). I tell my kids to think of one side of the multiplication as an object, like “five cents”, and then the other side is how many times to count that object. For me that is repeated addition and that’s how I get zero fives. You can even write it out, 3X5 = 5+5+5 and 0 X 5 is just nothing there (equals zero, because zero is a number). I would not say “added to itself” because that seems to presuppose at least one. Maybe I don’t get repeated addition. If you have to say “added to itself” then that could definitely be confusing and I would agree with you! But, I still would teach multiplication as counting objects, which is exactly how I teach addition (incrementing).
No, I disagree with you. A child asking a question is a good thing! You do realize that if they talk to you, you can help them. It’s never too late to explain how to get from words to the math symbols.
Also, I want to challenge you to rephrase the this-per-that.
A child asking a question is a beautiful thing. I love teaching through discussion.
But a child who has so little understanding of the math they have been taught that they ask *that* question is a tragedy. It means they have wasted long hours of time following instructions like a little robot with no sense of the meaning behind their actions. Better not to study math at all than to do that.
I guess that is a different kind of question they ask, out of ignorance, I’m not sure I would assume the child had spent all that time following instructions. That would mean no one cared to be sure they were learning.
It seems like I am just tired of all this educational psychology discussion. Who really knows how we learn? Maybe the student had more than just math problems in their life. I’d like to think this student asking even “that” question deserves some help with math, maybe one on one. Who knows- maybe it takes our whole life-time a lot of time to figure out what multiplication and other math concepts mean and how to use them. I didn’t really start reading and exploring math until I had been out of college a few years and had time to find things to read from all kinds of topics in mathematics.
Anyway, my point is- it doesn’t have to be a tragedy. It might not be up to you, the new teacher necessarily, however, that same misguided student still has hope if they can get some remedial help.
Hi Denise,
You do know how multiplication works. You have creative ways of describing how to think about it. I’m sure you draw from the many times you have used story/word problems to get the student to see what multiplying does.
I have a very visually-oriented daughter who is learning. algebra now. I found a DK book called,”How to Be Good at Math, The simplest-ever visual guide”
On page 98, it has “Multiplication:
There are two main ways to think about how multiplication works. We can think of it as putting together, or adding,lots of quantities of the same size.We can also think of it as changing the scale of something.”
On page 100,” Multiplying as scaling:
When we change the size of an object, we carry out a kind of multiplication called scaling. We also can use scaling when we multiply fractions.
I think you described both of these ways of thinking, only in your own
words. I think the book helped me because it had drawings. So, thank you for getting me to really look at what we do with multiplication.
Actually, I’m really not concerned with whether multiplication “is” or “is not” repeated addition. That debate (which still rages off and on in various blogs) is merely my excuse for analyzing how we teach multiplication — and specifically, for pointing out that we must teach it in a way that distinguishes it from addition.
The saddest thing that I have seen in my math classes is the student who reads a simple, one-step word problem and gets a glazed look in her eyes. Then she looks at the teacher for guidance and asks, “Do I add or multiply?”
It breaks my heart that a child can learn to crank through mathematical steps and procedures and yet have so little understanding of what she is doing.
We must teach our students how to recognize a multiplicative situation when they meet it in a word problem. And the best way that I know to teach such recognition is to point out and help students notice the multiplicand, the this-per-that ratio.
Here here to that. It is very sad, generally, when children “learn” to deal with problems by simply matching up the data they see with the tools they have. See this in physics all the time. “Oh, I have a mass and a force in the problem, I will use my formula Mass X Force = Acceleration”. If they have two formulas memorized for the same variables then they are forced to guess because they truly have no idea what to do.
“This per that”is not a ratio. I do not understand that wording.
Homeschool math calls it,”The SAME amount of something IN EACH thing is often solved by multiplying.
So, for example there are five children. Each child has 3 apples. How many apples are there? You need to find out by multiplying the number of apples per child by the number of children. Why confuse them with the word ratio? Or do you not use the word ratio, just the “this per that” in the word problem? As a mathematician, I look at all the definitions of words in a math dictionary. It seems to help me think about what multiplication is, here.
Even when we don’t agree or go off on a tangent, I learn something.
I guess I forgot you had a chart for “this per that” – still seems weird out of context. And now I’m thinking about fractals! That’s a good thing. Variety in learning math helps keep everyone’s interest.
Thank you for the link to the Natural Math poster of multiplication. You have become a great resource to me.
You’re welcome! The Natural Math folks have *so* many great resources for learning math in playful ways. https://naturalmath.com/
I love this discussion! (I stumbled upon it today while looking for something else.) Thank you Denise for expounding on some of the many ways students have to understand multiplication.
There are a couple of things that I would like to add to the conversation about the misquote of my definition above. The actual definition stated in “Elementary Mathematics for Teachers” is:
Definition 5.1. Multiplication of whole numbers is repeated addition: 3×5=5+5+5 } 3 times.
(You have to imagine the “} 3 times” as a bracket underneath the 5+5+5.)
The equation 3×5 = 5+5+5 is an important and inseparable part of the actual definition. The equation is designed to give meaning to the term “repeated definition.” Without the equation, the term “repeated addition” is completely meaningless as Denise points out with some nice examples of series. (To be honest, it was a bit of a shock to be quoted as saying that “repeated addition” was the entire definition, which is why I had to respond.)
The reasons for including the term “repeated addition” at all when we wrote the book were a bit complicated. Let’s just say here that we were trying to “commandeer” the term in order to give it a reasonable meaning. (For example, Tom and I were getting tired of seeing it claimed to mean, “Add 5 to itself 3 times,” which leads to the expression 5+5+5+5.)
The second issue is just how important the words “whole numbers” are in Definition 5.1 above. We are not claiming in our definition to give meaning to fraction, integer, or real number multiplication, or give meaning to scaling, area, or ratio versions of multiplication—only whole number multiplication. And of course, the definition is just the “formal” aspect of it: we back up the definition with lots of examples and models that help give the definition meaning in that section. Our books are set up to lead teachers (and parents) through the development process by following the Singapore Math textbooks grade-by-grade, and K-5 students are first exposed to multiplication in terms of whole numbers in grade 1. As we march through later grades in our books we expand and develop a much richer understanding of multiplication.
Hope this helps! (On a side note: I should have a 3-part video series with my daughter on my website soon where she explains how she learned to multiply whole numbers when she was 4 years old. Should be fun.)
Scott, I’m so sorry that you felt I misquoted your book! I’ve edited the article to add an ellipsis and included a photo of the actual definition entry. Does that help?
It was certainly not my intention to pick on your book’s treatment of multiplication, but rather to let it stand as representative of the approach that the great majority of elementary textbooks take. The way you define “repeated addition” is exactly what everyone means by the term: that one of the factors is added to itself repeatedly, and the other factor names the number of addends. Even the people who are careless with their wording mean it to be taken that way.
And the repeated addition model can be successfully extended beyond whole numbers. For instance, one can easily imagine 3.5×5 as 5+5+5+(half of 5).
My primary complaint against defining multiplication as repeated addition is that tying the operations together that way doesn’t help students distinguish between them. In order to build a robust understanding, kids need to focus on the differences between multiplication and addition, not on the similarities (or the fact that one can be used to calculate the other).
Thank you for mentioning your videos! I didn’t know you had a blog, so I’m happy to find out about it. Now if I could just convince my rss reader to recognize the feed…
No worries! I just wanted to make it clear that I’m also NOT a fan of just stating “repeated addition” whenever someone asks what multiplication is without carefully explaining exactly what you mean by the term.
Mathematicians actually treat addition and multiplication as two separate operators in abstract settings that may or may not be “related” to each other like they are for whole numbers (think matrices). The fact that the operators are related for whole numbers (cf. Peano) through “repeated addition” does, however, have consequences for teaching students multiplication of whole numbers. While I totally agree with you that a great way to help someone learn a new concept is by discussing how it is different from another already-learned concept, it is also important for the learner to appreciate how two concepts are related when they are related.
Yes! Thank you. Scott, I am going to look for your teaching materials.
Interesting posts! When introducing a new topic, in this case the operation of multiplication, I think it is important to connect it with previous knowledge first by pointing out the similarities and then the differences. I would start by motivating multiplication as a way to encode “repeated addition,” for instance you may ask to add the following numbers:
5+5+5 =
3+3+3+3+3 =
7+7 =
2+2+2+2+2+2+2 =
Children can find out the answers using addition and then note how much space and time it takes to repeatedly write down so many of the same number, especially the 7 twos. So to make things easier to write down we use a new operation called multiplication. In place of 5+5+5 we write 3 fives or 3 x 5 (read as 3 times 5), where 3 indicates how many fives you are adding. Then you ask them to fill out the alternate way of writing each of the above exercises using the new operation of multiplication:
5+5+5 = 3 fives = 3 x 5
3+3+3+3+3 = 5 threes = 5 x 3
7+7 = 2 sevens = 2 x 7
2+2+2+2+2+2+2 = 7 twos = 7 x 2
To make the distinction more clear between the multiplier and multiplicand, I think it’s nice to write the multiplicand in words rather than as a number (I can see this helping down the road with factoring as well for instance). Then you can ask them to find the answers to
3 x 5 =
5 x 3 =
2 x 7 =
7 x 2 =
Ask them: Why is 3 fives the same as 5 threes? Why is 2 sevens the same as 7 twos? Hand them cuisenaire rods and help them see how the rectangles formed in each case fit together. Also do it in the number line as explained in Vi Hart’s video:
Thanks for dropping by, Sandi!
There are so many different ways to approach multiplication, aren’t there? But the important thing, as you said, is to think about connections between math ideas. I really like the video you shared. 🙂
When my kids are just starting out with multiplication, we tend to use simple models, as I explain in the next post in this series.