
Poster by Maria Droujkova of NaturalMath.com. In this Homeschooling Math with Profound Understanding (PUFM) Series, we are studying Elementary Mathematics for Teachers and applying its lessons to home education.
Multiplication is taught and explained using three models. Again, it is important for understanding that students see all three models early and often, and learn to use them when solving word problems.
— Thomas H. Parker & Scott J. Baldridge
Elementary Mathematics for Teachers
I hope you are playing the Tell Me a (Math) Story game often, making up word problems for your children and encouraging them to make up some for you. As you play, don’t fall into a rut: Keep the multiplication models from our lesson in mind and use them all. For even greater variety, use the Multiplication Models at NaturalMath.com to create your word problems.
Study Teaching Materials
In this section, our textbook refers to Singapore Primary Math 3A pp. 68-90. It seems to me that the following would also be helpful, if you have these books: 1B pp. 42-53; 2A pp. 68-71, 80-91; 2B pp. 20-35; 3A pp. 39-56, and 68-90. Page numbers are from my (old!) 3rd edition books. If you have a different edition or another textbook series, look for headings like these:
- Multiplication
- Equal Groups
- Multiplication and Division
- Word Problems
By following the topic through several grade levels, you will get a better understanding of how your textbook series develops a student’s understanding. Pay attention to how the concepts are introduced and how they are built up step by step from one lesson to the next. Does your textbook push students straight into memorization drills, or does it encourage the use of a variety of thinking strategies?
Three Basic Multiplication Models
Elementary Mathematics for Teachers discusses three basic models, or mental pictures, that are helpful for teaching multiplication to your children.
(1) Set Model
“_____ sets of ______ objects per set”
This model represents discrete (countable) items collected into groups: apples per basket, pennies per dime, or cookies per plate. The set model includes the idea of multiplication as repeated addition, so it is the most common way of introducing multiplication to young children.
(2) Measurement Model
“_____ units of _____ measures per unit”
This model represents continuous quantities measured out in parts: inches per foot, cups per recipe, dollars per pound, or spaces per jump on a number line. The measurement model can include the idea of multiplication as scaling, stretching, or shrinking something from its original size, which makes it useful when thinking about fractions.
(3) Rectangular Array Model
“_____ rows of _____ items per row”
In early elementary math, the this model represents an array of discrete items: chairs per row, buttons per column, or soldiers on parade. As students grow, however, the model expands to include continuous rectangular area. At its most mature, this model becomes the basis for many topics in high school math and beyond, including integral calculus. Because of its flexibility, the rectangular model is the most important one for our children to master.
Notice that in each model, the two numbers of a multiplication problem have different roles. The first number is a scale factor, which tells you how many sets, units, or rows you are talking about, while the second number is a this-per-that ratio. In addition and subtraction, both numbers must represent the same type of thing, but this is almost never true in multiplication and division. Even in rectangular area, where both numbers represent a length measurement, one must be the horizontal length and the other vertical (the x- and y-dimensions in coordinate graphing).
Multiplication Model Games
I have created a deck of cards representing the three models of multiplication, so that your children can master them by playing games.
Or pick up the free Multiplication & Fraction Printables file, with a full-color multiplication model card deck and much more.
The cards do not include every math fact on the times table, but they should provide enough variety to cement the multiplication models in your children’s minds.
For a quick and easy game using the multiplication cards, play Concentration: Lay all the cards face down on the table, then try to turn up two matching cards — any two cards that belong to the same math fact. For young children, try playing Concentration with the cards face up.
Or try Go Fish, according to your family’s favorite rules. At our house, we match in pairs (not sets of four) and allow a free turn whenever you draw the card you asked for from the fishing pond.
Both of these games help children grow comfortable with the multiplication models.
Properties of Multiplication
Proceeding through our textbook lesson, we meet our old favorite “Any Order” Property: Numbers may be multiplied in any order without changing the answer. Addition was both commutative and associative, too, so this property may seem rather boring to you, but don’t take it for granted. It should be surprising. In addition, we were combining two of the same sort of things, such as pushing together two piles of blocks, so it makes sense that the answer shouldn’t matter on order. But the idea that 3 baskets of 4 apples per basket contain the same number of apples as 4 baskets of 3 apples per basket — Wow!
Experiment with your children by making sets. Explore how the numbers work. Let your children discover and wonder at the amazing coincidence of the any-order property. And later, as they grow in understanding the multiplication models, use the rectangular array model to show why it will always be true. If you give the rectangle a quarter-turn, the rows and columns switch places, but the total number of items stays the same.
Now we meet a new principle: The Distributive Property: Any number times a sum is the same as the sum of the individual products (that number times each individual part of the sum). This is usually expressed in algebra.
The distributive property is one of the most basic rules of arithmetic. Think of it as the “shopping bag rule.” If you buy six bags of mixed fruit, and each bag contains three apples and two pears, then you bought 6 × 3 apples and 6 × 2 pears. The parentheses act like grocery bags.
- Fruit in mixed bags = fruit sorted by type:
6 × (3 + 2) = (6 × 3) + (6 × 2)
The distributive property is definitely “fundamental mathematics,” so we need to become familiar with it and recognize it in many situations. One thing that impressed me in the Liping Ma book is how often the Chinese teachers called on the distributive property to explain what they were doing and how blind the American teachers seemed to be to it.
I remember in the New Math textbooks of my childhood we spent many lessons trying to master the words “associative,” “commutative,” and “distributive” and tell which property was represented by a certain equation. It was tremendously confusing, even to a good math student, and there is no reason to torture our children this way. The important thing is to learn the principles and be able to use them, not to memorize definitions and rules.
Teachers should know and use the terms “distribute” and “distributive” so children get used to them, but I wouldn’t expect the students to remember the terms until pre-algebra or algebra.
The arithmetic properties are taught as principles about the ways that whole numbers behave; they are illustrated with models using specific numbers and are practiced with Mental Math and word problems. They are not “rules” to be memorized.
— Thomas H. Parker & Scott J. Baldridge
Elementary Mathematics for Teachers
Thinking Strategies for Multiplication
I wrote extensively about the thinking strategies for multiplication in my Times Table Series, so I won’t repeat any of that here.
One thing that I do with my students, usually in 3rd or 4th grade, is to give them a bunch of blocks (unit base ten blocks, but any small manipulative that can be lined up in a rectangular array would work) and several sheets of graph paper. I have them draw all the rectangles they can make for each set of blocks from 1 to 100, or as far as they can get in a few days’ worth of work. They will discover that 12 makes the 1×12, 2×6, and 3×4 rectangles, while 13 only makes 1×13. They can see exactly what square numbers are and why they have that name, and how prime numbers are different from composite numbers. This is early practice in factoring, which will be important in later math work.
Three Stages of Learning Multiplication
Because I prefer to delay formal arithmetic, with its emphasis on rules and memorization, I see these stages as stretching out longer than what our textbook authors recommend. My goal is the same: fluency in using multiplication to solve problems. But I prefer to spend the early- to mid-elementary years in the “figuring it out” stages (Stage I and Stage II by our book’s system) and let my children count blocks, fingers, or tally marks while we talk together about thinking strategies — and work lots and lots and lots of informal, oral story problems.
Stage I
(preschool-grade 2)
No pressure to memorize facts in this stage, because the focus is on understanding what multiplication is (and its inverse relationship with division) and learning to recognize a this-per-that ratio. Use plenty of pictures and word problems.
Stage II
(grades 2-4)
The emphasis is on deepening the student’s understanding, using all the models of multiplication, and learning to do multi-step problems. Memory work begins, but it is definitely not the main focus. Mental manipulation of numbers, using what you know to figure out what you don’t know, builds deep familiarity with the math facts and fundamental properties of multiplication. Notice for example the paragraph on the top of p. 29, where the problem 7 × 14 = 98 is used to show the significance of understanding and using place value and the distributive property.
Stage III
(grades 3-whenever)
Wrap up the memory work, using games to make drill-style practice fun. The time needed will vary from one student to another, but I try to bring my children to readiness for this stage by 4th grade and to mastery by the end of 5th, if possible. I agree with our textbook authors’ statement that “Confidence is a major factor in learning and enjoying mathematics,” but it is possible to enjoy and excel at math even if one never masters all the multiplication facts. Consider this oft-quoted anecdote:
Ernst Eduard Kummer (1810-1893), a German algebraist, was rather poor at arithmetic. Whenever he had occasion to do simple arithmetic in class, he would get his students to help him. Once he had to find 7 × 9.
“Seven times nine,” he began, “Seven times nine is er — ah — ah — seven times nine is…”
“Sixty-one,” a student suggested. Kummer wrote 61 on the board.
“Sir,” said another student, “it should be sixty-nine.”
“Come, come, gentlemen, it can’t be both,” Kummer exclaimed. “It must be one or the other.”
— quoted from Anecdotes About Famous Scientists
Homework Set 5
I’ve gone so long that I won’t comment on the homework problems, except to say that problem 8 demonstrates why older children should have scratch paper (or a white board and markers) available while working with mental math, to make notes or write down the answers of intermediate steps. Most people can’t hold that much information in short-term memory.
Times table by David Millar.
* * *
“PUFM 1.5 Multiplication, Part 2” is part of the Homeschooling with a Profound Understanding of Fundamental Mathematics Series. Go to the previous post. Or start at the beginning.
This blog is reader-supported.
If you’d like to help fund the blog on an on-going basis, then please head to my Patreon page.
If you liked this post, and want to show your one-time appreciation, the place to do that is PayPal: paypal.me/DeniseGaskinsMath. If you go that route, please include your email address in the notes section, so I can say thank you.
Which I am going to say right now. Thank you!
“PUFM 1.5 Multiplication, Part 2,” copyright © 2012 by Denise Gaskins.
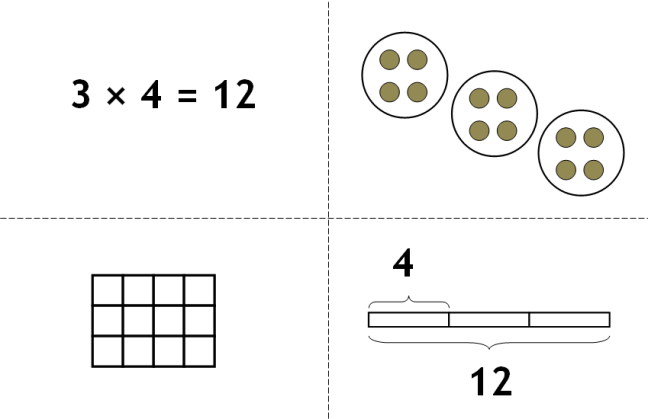
Thanks so much for this post and the game. I posted a thank you on the Living Math Forum a few days ago but it hasn’t gone through yet, so I wanted to let you know here, too. I’ve been thinking for a month or so that my daughter (7) needed to move forward with arithmetic — she’s got metal addition/subtraction down now and is less inspired by the card games — but I wasn’t quite sure how to proceed. Three different games with the same cards is just the ticket. It’s also fabulous to have some language to use, the big picture of multiplication/division (stuff I never really got in my own schooling) and also the reminder about math stories!!
Thank you. This all makes sense! I totally agree teachers should know the properties- I learned them somewhere along the way.
Anyway, stay away from part 1; part 2 is much better.
This is the place to find out everything about multiplication. Part 1 explores the the model of multiplication as repeated addition.